Odwrotny efekt Comptona

Dla fotonów ultrarelatywistycznych pochodzących źródeł synchrotronowych emitowana moc staje się bardzo nieizotropowa i następuje rozpraszanie Thomsonowskie, które dostarcza energii fotonom kosztem energii elektronów. Fotony zostają przeniesione do zakresu optycznego, czy wręcz promieniowania X.

Relatywistyczne fotony są przenoszone na pewną częstotliwość, której średnia wartość wynosi:

$$\frac{<\nu>}{\nu_0} =\frac{4}{3}\gamma^2$$

$\nu_0$ - początkowa częstotliwość
$<\nu>$ - częstotliwość na którą zostały przeniesione fotony (wartość średnia, bo każdy foton na trochę różnią)

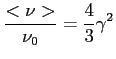
Zaś maksimum znajduje się na częstotliwości:

$$\frac{\nu_{max}}{\nu_0} =4\gamma^2$$

Całkowita moc, którą zyskał foton, a stracił elektron wynosi:

$$P_{IC}=\frac{4}{3}\sigma_Tc\beta^2\gamma^2U_{rad}$$

$\sigma_T$ - przekrój Thomsona
$U_{rad} = \vert\vec{S}\vert/c$ - gęstość energii padającego promieniowania
$\vec{S}$ - wektor Poyntinga

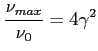
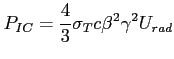
Wnioski:
Jeśli odwrotny efekt Comptona pochodzi od fotonów z emisji synchrotronowej (synchrotron self-Compton radiation) to wynikiem jest takiego samego kształtu widmo, przesunięte tylko w stronę wyższych energii.

Dla niespójnego źródła synchrotronowego tj. poszczególne obszary w źródle emitują falę e-m niezależnie od siebie (spójnym jest np. pulsar) oznacza to limit na temperaturę jasnościową (przy większej za szybko byłyby tracone fotony):

$$T_b \simeq 10^{12}~K$$

Przykładem jest efekt Sunyaev-Zel'dovich'a. Mikrofalowe promieniowanie tła jest zmienione przez zderzenia z energetycznymi elektronami gorącego gazu gromad galaktyk w odwrotnym efekcie Comptona. Przez co ilość promieniowania na niższych częstotliwościach zmniejsza się, a nadwyżka jest obserwowana na wyższych częstotliwościach. Znając własności ośrodka (dzięki obserwacji na falach X, które zależą od $N_e^2L$) można otrzymać odległość do gromady galaktyk.
 
Na falach radiowych rezultatem jest zmierzenie zmiany temperatury (absorpcja promieniowania), która wyraża się wzorem:

$$\frac{\Delta T}{T}=\frac{2kT_e}{m_ec^2}\sigma_T N_eL$$

$L$ - grubość ośrodka wzdłuż linii widzenia
$N_e$ - gęstość elektronowa, $[cm^{-3}]$
$T_e$ - temperatura elektronowa, $[K]$
$\sigma_T$ - przekrój Thomsona elektronu

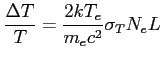
Ilustracja tego efektu: