Magnetobremsstrahlung

Już w 1992 teoretyczne badania Schott'a przewidziały, że poruszający się w polu magnetycznym ładunek emituje energię.
- elektrony (jako najlżejsze cząstki) przyśpieszane w polu magnetycznym
- większość emisji radiowej dla AGN, zaś dla niskich częstotliwości ( $\nu<30~GHz$) dominuje w emisji od normalnych galaktyk jak Droga Mleczna.
- pozwala wyznaczyć jedynie transwersalną (prostopadłą do nas) składową pola magnetycznego

1. Cyklotronowe

Przypadek nierelatywistyczny, stąd działa zwykła siła $F=\frac{e}{c}\vert(\vec{V}\times \vec{B})\vert =\frac{e}{c} V_{\bot}B= m\omega^2R$. Siła magnetyczna odpowiada za zakrzywienie toru cząstki (stąd cząstki krążą wokół linii pola magnetycznego) i częstość kołowa z tym związana wynosi:

$$\omega_G = \frac{eB}{m_0c}$$

$m_0$ - masa elektronu

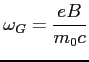
Stąd tzw. częstotliwość gyroskopowa (electron gyro frequency), równa częstotliwości orbitalnej dla V « c:

$$\nu_G = 2.8~B$$

$B$ - pole magnetyczne, $[Gauss]$
$\nu_G$ - częstotliwość, $[MHz]$
źródło wtedy emituje bądź absorbuje tylko tę częstotliwość (czy jej proste harmoniczne).
 
 
 
 
 
 
 
 
 
Przykład dla Jowisza:

Generalnie jest to zjawisko widoczne tylko dla najsilniejszych pól jak pulsar.
 

2. Synchrotronowa
a) Formuła Larmora:

Dla emisji synchrotronowej trzeba koniecznie uwzględnić efekty relatywistyczne (np. zmiana masy elektronu). Zatem przy braku pola elektrycznego:

$$\frac{e}{c}(\vec{V}\times \vec{B})=\frac{d\vec{p}}{dt}=\frac{d( \gamma m_0 \vec{V})}{dt}$$

$\vec{p}$ - wektor pędu
 
Stąd częstość wyraża się wzorem:

$$\omega = \frac{eB_{\bot}}{mc} = \frac{eB_{\bot}}{\gamma m_0 c}$$

$B_{\bot}$ - składowa pola prostopadła do trajektorii elektronu
 
Elektron jest przyspieszany w kierunku prostopadłym do $\vec{B}$ i amplitudę tego przyspieszenia można oznaczyć jako:

$$\omega_B=a_\bot/V_\bot$$

Związek między tą częstotliwością, a częstością gyroskopową wyraża się wzorem ( $\omega_B < \omega_G$):

$$\omega_B=\omega_G/\gamma$$

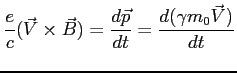
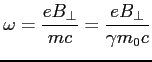
Częstotliwość wynosi:

$$\nu_B = \frac{eB_{\bot}}{2 \pi \gamma m_0 c}$$

$\gamma$ - czynnik Lorentza: $\gamma = \frac{1}{\sqrt{1-\beta^2}}$
$\beta=V/c$ - stosunek prędkości cząstki do prędkości światła w próżni
$m_0$ - masa spoczynkowa elektronu

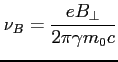
Promień trajektorii wyraża się wtedy wzorem:

$$R=\frac{\gamma m_0c^2 sin\alpha}{eB}$$

Zatem dla relatywistycznego elektronu o energii 10 GeV, znajdującego się w polu ISM $3~\mu G$ wynosi on ok. 7 AU.

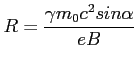
Wtedy relatywistyczna formuła Larmora tj. moc wypromieniowana przez elektron:

$$P = \frac{2}{3}\frac{e^2{a'_\bot}^2}{c^3} = \frac{2}{3}\frac{e^2{... ...ot}^2 \gamma^4}{c^3} = \frac{2}{3}\gamma^2\frac{e^4B^2}{m_0^2c^5}V^2sin^2\alpha$$

$\alpha$ - kąt między $\vec{V}$ a $\vec{B}$, (pitch angle)
Wyrażając $\alpha$ wzorem:

$$tg\alpha = \frac{V_\bot}{V_{\vert\vert}}$$

 
Formułę można potem uśrednić po kącie.

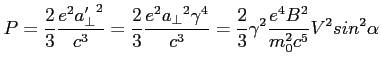
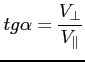
Często zamiast samego pola magnetycznego używa się jego gęstości energii pola magnetycznego:

$$U_B=\frac{B^2}{8\pi}$$

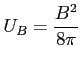
Zaś zamiast podstawowych wielkości opisujących elektron - przekrój czynny Thomsona (Thomson cross section) dla elektronu. Określa on prawdopodobieństwo zajścia rozproszenia, a zdefiniowana jest jako pole powierzchni (mierzone na płaszczyźnie prostopadłej do kierunku ruchu cząstki) w które musi trafić cząstka, by doszło do rozproszenia:

$$\sigma_T = \frac{8\pi}{3}\left( { \frac{e^2}{m_ec^2} }\right)^2 = 6.65\cdot10^{-25}~cm^2$$

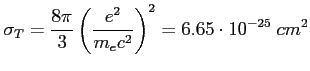
Przekrój Thomsona jest też potrzebny do oszacowania głębokości optycznej dla elektronu na rozpraszanie (niezależnie od emisji synchrotronowej):

$$\tau = \int \alpha ds = \int \sigma_T N_e ds$$

$N_e$ - gestość elektronów, $[cm^{-3}]$

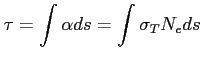
Widać, że dla rozpraszanie jest to wielkość niezależna od częstotliwości, a zatem istnieje taka częstotliwość dla której to rozpraszanie jest istotniejsze niż od innych procesów.

Stąd wypromieniowana przez elektron moc:

$$P=2\sigma_T\beta^2\gamma^2cU_Bsin^2\alpha$$

Co po uśrednieniu po kącie dla bardzo dużych prędkości $\beta^2\simeq 1$ (trzeba pamiętać, że $\gamma$ jest funkcja częstotliwości!) daje:

$$P=\frac{4}{3}\sigma_T\beta^2\gamma^2cU_B$$

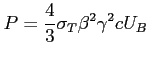
b) Czas chłodzenia elektronu:
Elektron ma energię $E=\gamma m_ec^2$, którą powoli traci (elektron się chłodzi). Dzieląc energię elektronu przez moc wypromieniowaną przez elektron można oszacować czas chłodzenia elektronu i przez to zobaczyć czy obiekt ma świeże źródło energii:

$$\tau_{col}=\frac{E}{P} = \frac{3m_ec^2}{4\sigma_T c U_B \gamma \beta^2}$$

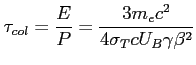
c) Widmo pojedynczego elektronu:
Elektron krąży, po bardzo dużej orbicie stąd w zależności od kąta $\alpha$ jest krótko bądź długo (wręcz ciągle) skierowany na nas. Elektron w swoim własnym układzie odniesienia ma symetryczną charakterystykę mocy (taką jak dipol), ale w układzie odniesienia obserwatora, względem którego prędkość elektronu jest relatywistyczna, ma on charakterystykę wydłużoną i zwężoną w stronę swojej prędkości (beaming). Choć moc wyemitowana w obu układach odniesienia musi być taka sama - zmianie ulega tylko charakterystyka mocy. Pokazuje to rysunek:

Stąd widzimy promieniowanie z bardzo wąskiego kąta ($\gamma>>0$):

$$\theta = 2\phi = \frac{2}{\gamma}$$

Co daje typowy czas pulsu :

$$\Delta t \simeq \frac{1}{ \gamma^3 \omega_B sin\alpha}$$

Oraz odstęp między pulsami:

$$t = \frac{2\pi}{\omega_G}=\frac{1}{\gamma \nu_B}$$

$\nu_G$ - częstotliwość gyroskopowa
 
W obu przypadkach w środku znajduje się zależność od kąta, stąd ten czas pulsu może przy danym polu magnetycznym być bardzo różny.

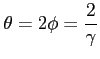
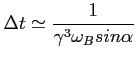
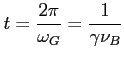
To daje częstotliwość dla której cząstka promieniuje najwięcej energii:

$$\nu_{max}\simeq \frac{1}{2\pi \Delta t}$$

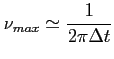
Obserwowane widmo POJEDYŃCZEGO elektronu jest transformatą Fouriera z kształtu pojedyńczego pulsu (poszczególne harmoniczne są tak blisko, że widmo staje się ciągłe). Wynikiem jest widmo mocy (aby otrzymać strumień trzeba podzielić przez pole powierzchni orbity obserwatora tj. $4\pi d^2$, gdzie d - odległość do obiektu). Moc spektralna WYEMITOWANA przez pojedyńczy elektron:

$$P_1(\nu) = \frac{\sqrt{3}e^3Bsin\alpha}{m_0c^2} \left( {\frac{\nu}{\nu_c}}\right) \int_{\nu/\nu_C}^{\infty} K_{5/3} (\eta) d\eta$$

$$P_1(\nu) \simeq \frac{\sqrt{3}e^3Bsin\alpha}{m_0c^2} \left( {\frac{\nu}{\nu_c}}\right)^{1/3} e^{-({\nu}/{\nu_c})}$$

Jednostka: $[W/Hz]$
$K_{5/3} (\eta)$ - zmodyfikowana funkcja Bessela
$\alpha$ - kąt między $\vec{V}$ a $\vec{B}$

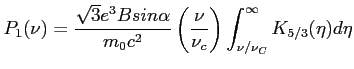
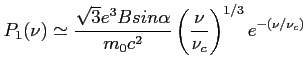
Użyta częstotliwość krytyczna (cut-off frequency or critical frequency) to częstotliwość oscylacji plazmy, zależna od gęstości elektronowej. Poniżej niej fala zostaje odbita, a powyżej przechodzi przez ośrodek.

$$\nu_C = \frac{3}{2}\gamma^2\nu_G sin\alpha = \frac{3}{2}\gamma^3\nu_B sin\alpha =16.08\cdot 10^6 B_{\bot} E^2~MHz$$

$E$ - energia elektronu, $[GeV]$
$B_{\bot}$ - pole magnetyczne, [G]
 
Związek że współczynnikiem załamania dla plazmy:

$$n=\sqrt{1-\left( {\frac{\nu_c}{\nu}}\right)^2 }$$

$\nu>\nu_c$ - fala e-m rozchodzi się w ośrodku ($n<1$)
$\nu<\nu_c$ - fala e-m odbija się ($n=0$ lub zespolone)

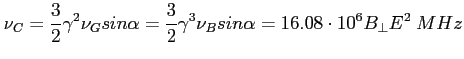
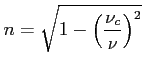
Rysunek pokazujący widmo jednego elektronu, gdzie $x={\nu}/{\nu_c}$, zaś $F(x) = \left( {x} \right)^{1/3} e^{-x}$, a zatem pokazuje kształt tego widma. Widać, że dla niskich częstotliwości nachylenie wynosi 1/3.

Maksimum w okolicach $\nu_{peak} = 0.29\nu_c$

d) Widmo rozkładu elektronów
Obserwowany rozkład energii elektronów pochodzących z promieniowania kosmicznego i okazuje się, że od kilku GeV jest potęgowy (w Galaktyce, dla reszty zakładamy, że podobnie):

$$N(E)dE \simeq N_0 E^{-\delta} dE$$

$N(E)dE$ - liczba elektronów na jednostkę objętości z zakresie energii od E do E+dE
$N_0$ - początkowa ilość elektronów w jednostce objętości
$\delta$ - dla naszej Galaktyki ok. 2.4 (inne spiralne $2.4\div3.0$)
$E=\gamma m_e c^2 = (\nu/\nu_G)^{1/2}m_e c^2$ - energia elektronu

Przedział energii $E_1<E<E_2$. Można założyć, że każdy elektron wypromieniowywuje całą moc P w jednej częstotliwości $\nu = \gamma^2\nu_G$.

Ogólnie zdolność emisyjna dystrybucji elektronów:

$$j_\nu d\nu = - \frac{dE}{dt}N(E)dE = -P N_0 E^{-\delta} \frac{dE}{d\nu} d{\nu}$$

Po podstawieniu:

$$j_\nu = - \left( {\frac{4}{3}\sigma_T \beta^2 \gamma^2 c U_B}\right) (N_0 E^{-\delta}) \left( {\frac{m_ec^2\nu^{-1/2}}{2\nu_G^{1/2}}}\right)$$

Co daje:

$$j_\nu \sim (B sin\alpha)^{(\delta+1)/2}\nu^{(1-\delta)/2}$$

Zatem związek $\delta$ z indeksem spektralnym:

$$\alpha = \frac{\delta-1}{2}$$

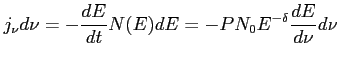
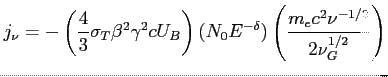
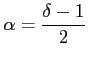
d) Indeksy spektralne
Zatem w obszarze optycznie cienkim (wysokie częstotliwości) ta zależność przenosi się na zależność strumienia $\left(j(\nu) \sim S(\nu)\right)$ od częstotliwości. Stąd, ponieważ dla naszej galaktyki $\delta = 2.4$ oznacza to indeks spektralny $\alpha \simeq 0.7$, gdzie $S\sim\nu^{-\alpha}$. Jest to zgodne z obserwacjami dla wielu źródeł np. kwazarów.

$$S_\nu \sim B^{\alpha+1}\nu^{-\alpha}$$

W obszarze optycznie grubym ($\tau>>1$, niskie częstotliwości) dla idealnego, jednorodnego źródła następuje odwrócenie widma spowodowane samoabsorpcją. Jest ona istotna dla w bardzo jasnych, zwartych źródłach. Związana jest ona z absorbcją fotonu przez elektron (który jest reemitowany na wyższych częstotliwościach i może też prowadzić do emisji wymuszonej). Proces jest proporcjonalny do intensywności promieniowania. Wiedząc, że współczynnik absorpcji wynosi :

$$\alpha_\nu \sim B^{\frac{\delta+2}{2}}\nu^{-\frac{\delta+4}{2}}$$

Z prawa Kirchhoffa można wyliczyć strumień:

$$B_\nu = j_\nu / \alpha_\nu$$

Po podstawieniu daje to dla Galaktyki ( $\delta = 2.4$) indeks spektralny $\alpha \simeq -5/2$.
W praktyce jednak indeks ten jest niższy że względu na różne niejednorodności np. niejednorodne pole magnetyczne jak i głębokość optyczna pochodząca od różnych fragmentów źródła.
Są to zależności ogóle, ale współczynnieki, a zatem i same widmo zależy od tego czy pole jest regularne czy nieregularne.
 
- przykładowo dla 3c 48 (radio kwazar o plaskim widmie), widmo zaczyna być samoabsorbowane dla $\nu< 100~MHz$, zaś dla 3c 84 (rozlegla radiogalaktyka, o stromym widmie) $\nu< 20~GHz$


Polaryzacja:
Teoretyczny stopień polaryzacji liniowej dla emisji synchrotronowej przy jednorodnym polu magnetycznym wyraża się wzorem:

$$p=\frac{\alpha+1}{\alpha+5/3}$$

 
To dla typowego indeksu spektralnego $\alpha=0.75$ daje wartość 72% niezależnie od częstotliwości. Jest to niezgodne z obserwacjami (np. dla galaktyk spiralnych $p=0.1\div0.2$) co wynika częściowo z rotacji Faradaya rosnącej z długością fali jak i istotnych niejednorodności pola magnetycznego (różne wartości i kierunki pola na drodze do nas).
 
Statystycznie można zapisać:

$$p=p_H\frac{B^2_{reg}}{B^2}$$

$p$ - stopień polaryzacji liniowej
$p_H$ - teoretycznie wyliczony (z wzoru wyżej) stopień polaryzacji
$B_{reg}$ - pole regularne
$B$ - całkowite pole magnetyczne
 
Stąd może tylko 25% energii pola magnetycznego jest związane z wielkoskalowym składnikiem.
 
e) Źródła energii

Nie wiemy, czy emitowana moc wynika z dużego pola magnetycznego, czy dużej koncentracji promieniowania kosmicznego ($j$ zależy od obu wielkości w pewnych potęgach). a chcemy wiedzieć jaka minimalna energia jest potrzebna by wyprodukować źródło synchrotronowe o zadanej jasności. Stąd potrzebne są dodatkowe założenia. Całkowita energia dostępna dla emisji synchrotronowej to:

$$W_{tot}=(U_p+U_{B})V$$

V - objętość źródła
Zaś wielkości po prawej stronie to gęstości dwóch różnych rodzaji energii:
 
- pola magnetycznego:

$$U_B=\frac{B^2}{8\pi}$$

- promieniowania kosmicznego (elektrony, protony oraz inne jony). Przeważającym źródłem energii są elektrony stąd używa się:

$$U_p=\eta U_e$$

$U_e$ - gęstość energii elektronów
$\eta\simeq 100$ - czynnik biorący pod uwagę inne cząstki

$$U_e = \int_{E_{min}}^{E_{max}} E^{1-\delta} dE \sim B^{{n-1}/2}$$

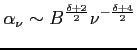
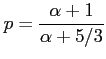
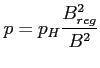
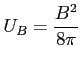
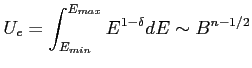
Generalnie przyjmuje się przedział częstotliwości: $\nu_{min}=10^7~Hz$ do $\nu_{max}=10^{11}~Hz$.

Nie umiemy zmierzyć wkładu obu składników stąd generalnie zakłada się, że poszczególne gęstości energii rozkładają się tak, że całkowita gęstość energii jest najmniejsza (dzieje się tak, gdy gęstość energii cząstek $\simeq$ 4/3 * gęstość pola magnetycznego). W ten sposób można ocenić zarówno energię cząstek jak i pole magnetyczne w źródle. Na emisję synchrotronową ma wpływ tylko składowa $B_{\bot}$, choć obserwacje dowodzą, że $B_{\bot} \simeq B_{\parallel}$.
 
Dla sferycznie symetrycznego źródła o objętości V i w odległości R, obserwowana gęstość strumienia będzie wynosić:

$$S_\nu=N_0H\frac{V}{R}B^{n+1}\nu^{-n}$$

$N_0$ - stała z dystrybucji elektronów w Galaktyce
$H$ - stała określona wzorem:

$$H=b(n) \frac{e^3}{mc^2}\left( {\frac{3e}{4\pi m^3c^5}}\right)^n$$

$b(n)$ - funkcja zależna on $\alpha$ (dla $\alpha <4$ $b(n)<0.5$, a dla $\alpha=2.5$ wynosi $0.12$)
 
Korzystając z założenia minimum energii prowadzi to do możliwości oszacowania pola magnetycznego że wzoru:

$$B_{eq}=\left( {6\pi \frac{G R^2}{HV}S_\nu \nu^n}\right) ^{2/7}$$

$G$ - stała określona wzorem:

$$G=\frac{\eta}{1-2\alpha}\left( {\frac{e}{m^3c^5}}\right)^{n-1/2}\left( {\nu_{max}^{1/2-\alpha}-\nu_{min}^{1/2-\alpha}}\right)$$

$\nu_{min}$,$\nu_{max}$ - zakres emisji synchrotronowej (tradycyjnie: 10 MHz $pm$ 100 GHz)
Te zależności po podstawieniu, dają również możliwość oszacowania minimalnej potrzebnej energii jak i wartość pola magnetycznego.
 
Drugim rodzajem założenia jest ekwipartycja energi, kiedy przyjmujemy, że gęstości energii magnetycznej i promieniowania kosmicznego są takie same, co daje podobne wartości.
 
Założenia dobre dla dużych skal przestrzennych i czasowych, natomiast dla małych skal są istotne odstępstwa.

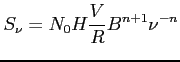
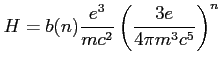
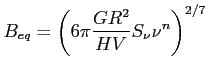
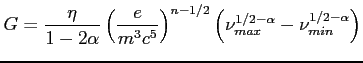
f) Oszacowanie masy i pola magnetycznego
Limit Eddingtona: minimalna masa potrzebna do wygenerowania danej jasności w całym paśmie radiowym [Watts] $L_E$, tak by grawitacja zrównoważyła ciśnienie promieniowania (limit przy którym akrecja staje się niemożliwa):

$$\left({\frac{L_E}{L_\odot}} \right) \simeq 3.3\cdot10^4~ \left({\frac{M_{min}}{M_\odot}} \right)$$

Zatem znając obserwowana jasność źródła można oszacować minimalną masę obiektu.
 
Maksymalna utrata masy:

$$\dot{M} = \frac{L_{E}}{c^2}$$

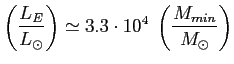
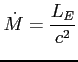
Oszacowanie pola magnetycznego dla niskich częstotliwości tj. ośrodka optycznie grubego $\tau>>1$ (tj. gdy temperatura elektronowa $T_e=E/3k$ jest równa temperaturze jasnościowej, a tak jest dla częstotliwości krytycznej (zależna od $T_b$)):

$$B \simeq 1.4\cdot10^{12} \nu_1 T_b^{-2}$$

$B$ - indukcja pola magnetycznego, $[G]$
$\nu_1$ - częstotliwość dla której źródło staje się nieprzezroczyste, $[Hz]$
$T_b$ - temperatura jasnościowa, $[K]$
 
Obserwacje pokazują, że temp. jasnościowe wielu pozagalaktycznych radioźródeł wynoszą $2.1\cdot10^{11}~K$., co między innymi świadczy o ich nietermicznym pochodzeniu.

Przykładowe widma radiowe kwazarów (o charakterze synchrotronowym):