Pochodzi od zjonizowanego gazu i zachodzących w nim przejściach swobodno-swobodnych. Oznacza to, że elektrony zakrzywiają tor czyli przyśpieszają podczas przechodzenia obok jonu, a każdy ładunek posiadający przyspieszenie promieniuje. Obszary tej emisji to przede wszystkim obszary HII (sfery Strömberga). Tworzą się one wokół gorących gwiazd (tak by było dużo fotonów jonizujących (UV) tj. o 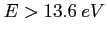 czyli większej od energii jonizacji wodoru) np. masywnych i młodych (O-B), białych karłów. Do zjonizowania otoczki trzeba gwiazdy o temp.
czyli większej od energii jonizacji wodoru) np. masywnych i młodych (O-B), białych karłów. Do zjonizowania otoczki trzeba gwiazdy o temp.
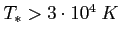 . Poniżej został przedstawiony bardzo uproszczony model, a raczej jego wyniki.
. Poniżej został przedstawiony bardzo uproszczony model, a raczej jego wyniki.
Temperatura elektronowa - inaczej kinetyczna. Dla plazmy wyznaczona z rozkładu Maxwella, co dla 3-stopni swobody daje
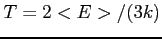 .
.
Rozmiar (przy założeniu kulistości mgławicy/otoczki) zjonizowanego obszaru wyraża się przez promień Strömberga (dalej znajduje się wąski obszar częściowej jonizacji, a potem obszar niezjonizowany) zależnym przede wszystkim od liczby jonizujących fotonów:
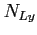 - ilość fotonów jonizujących (
- ilość fotonów jonizujących (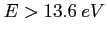 ) emitowanych na sekundę,
) emitowanych na sekundę, ![$ [s^{-1}]$](img552.png)
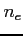 - gęstość elektornowa,
- gęstość elektornowa, ![$ [cm^{-3}]$](img82.png)
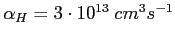 - parametr rekombinacji wodoru
- parametr rekombinacji wodoru
Obserwacje tych obiektów pozwalają oszacować przede wszystkim temp. elektronową (rzędu 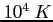 ) i gęstość elektronową w obiektach. W tym celu oblicza się głębokość optyczną, którą można przybliżyć wzorem:
) i gęstość elektronową w obiektach. W tym celu oblicza się głębokość optyczną, którą można przybliżyć wzorem:
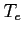 - temp. elektronowa,
- temp. elektronowa, ![$ [K]$](img535.png)
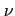 - częstotliwość,
- częstotliwość, ![$ [GHz]$](img558.png)
EM - miara emisji,
![$ [pc~cm^{-6}]$](img559.png)
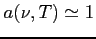 - niewielka poprawka
- niewielka poprawka
Miara emisji (emission measure) jest zdefiniowana jako:
Jednostka:
![$ [cm^{-6}pc]$](img562.png)
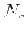 - gęstość elektronowa, ilość elektronów w jednostce objętości,
- gęstość elektronowa, ilość elektronów w jednostce objętości, ![$ [cm^{-3}]$](img82.png)
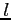 - rozmiar obłoku/mgławicy,Średnica,
- rozmiar obłoku/mgławicy,Średnica, ![$ [pc]$](img98.png)
Można też oszacować ilość fotonów jonizujących produkowanych przez gwiazdę w jednostce czasu:
Jednostka: ![$ [s^{-1}]$](img552.png)
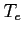 - temp. elektronowa,
- temp. elektronowa, ![$ [K]$](img535.png)
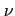 - częstotliwość,
- częstotliwość, ![$ [GHz]$](img558.png)
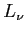 - moc spektralna dla wysokich częstotliwości (
- moc spektralna dla wysokich częstotliwości (
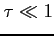 ),
),
![$ [W~Hz^{-1}]$](img388.png)
Posiadając temp. elektronową i głębokość optyczną można wyliczyć temperaturę jasnościową:
Wykres funkcji 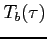 dla
dla
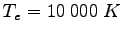 (typowy obłok wodorowy) przedstawia wykres:
(typowy obłok wodorowy) przedstawia wykres:
Przeliczając na strumień:
Widać, że obszar dzieli się na dwie części (oraz 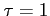 ):
):
- (1)
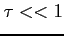 wysokie częstotliwości (zazwyczaj
wysokie częstotliwości (zazwyczaj
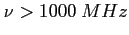 ), obszar prawie przezroczysty,
), obszar prawie przezroczysty,
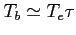 , stąd
, stąd
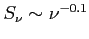
- (2)
 niskie częstotliwości (zazwyczaj
niskie częstotliwości (zazwyczaj
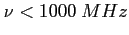 ),obszar optycznie gruby,
),obszar optycznie gruby,
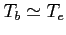 , czyli
, czyli
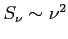 (w praktyce raczej niższy np. dla PN to ok. 0.6, bo obszary o niejednorodnej gęstości elektronowej)
(w praktyce raczej niższy np. dla PN to ok. 0.6, bo obszary o niejednorodnej gęstości elektronowej)
- (3)
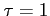 maksimum w widmie dla częstotliwości załamania (turnover frequency), dzieli oba wymienione obszary
maksimum w widmie dla częstotliwości załamania (turnover frequency), dzieli oba wymienione obszary
Wyznaczając częstotliwość 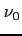 (wyrażoną w GHz), dla której głębokość optyczna jest równa jedności można posłużyć się wzorem:
(wyrażoną w GHz), dla której głębokość optyczna jest równa jedności można posłużyć się wzorem:
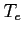 - temperatura elektronowa,
- temperatura elektronowa, ![$ [K]$](img535.png)
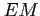 - miara emisji,
- miara emisji,
![$ [pc~cm^{-3}]$](img583.png)
Typowe wartości dla obłoku HII to
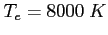 ,
,
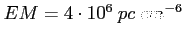 ,
,
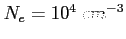 i
i
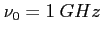 .
.
Przykładowe widmo mgławicy planetarnej:
Najogólniej - strumień przychodzący z obszaru zajętego przez źródło termiczne (np. mgławica planetarna + światło gwiazdy przechodzące przez mgławice):
Bogna Pazderska
2009-01-20
![]() .
.
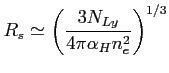
![]() ) i gęstość elektronową w obiektach. W tym celu oblicza się głębokość optyczną, którą można przybliżyć wzorem:
) i gęstość elektronową w obiektach. W tym celu oblicza się głębokość optyczną, którą można przybliżyć wzorem:
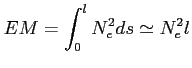
![\includegraphics[width=7cm]{Rysunki/tempB.eps}](img570.png)
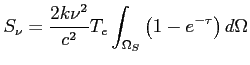
![]() ):
):
![\includegraphics[width=7cm]{Rysunki/051.4+09.6Q.eps}](img588.png)
![$\displaystyle S_\nu = \frac{2k\nu^2}{c^2} \left[ {T_e \int_{\Omega_S}\left( { 1 - e^{-\tau} } \right) d\Omega +T_b \int_{\Omega_S}e^{-\tau}d\Omega }\right] $](img589.png)