Next: Mechanizm ``free-free'' Up: Termiczne Previous: Termiczne Spis rzeczy
Zachodzi, gdy
![]() . Wtedy z równania transferu mamy zależność
. Wtedy z równania transferu mamy zależność
![]() . Głównie obserwuje się w bliskich obiektach jak w obrębie Układu Słonecznego.
. Głównie obserwuje się w bliskich obiektach jak w obrębie Układu Słonecznego.
Ogólna zależność - prawo Plancka
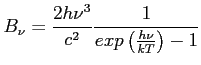
Przybliżenie stosowane generalnie (wyjątek: CMB) w radioastronomii (dla ![]() ) - prawo Rayleigha-Jeansa:
) - prawo Rayleigha-Jeansa:
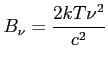
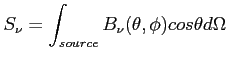
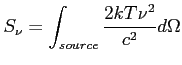
![\includegraphics[width=7cm]{Rysunki/blackbody.eps}](img531.png)
Innym rodzajem promieniowania, związanym z ciałem doskonale czarnym jest termiczna emisja od pyłu. Wzór na temperaturę jasnościową obiektu (same cząstki są bardzo małe):
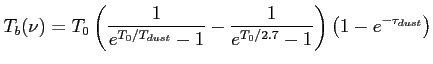
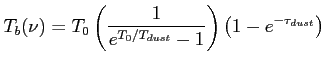
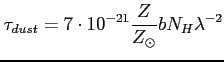
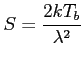
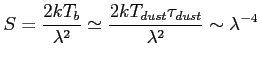
Jest to ważny wkład do promieniowania na wysokich częstotliwościach. Szacuje się, że gaz o temperaturze 100 K do 30 K stanowi większość masy naszej Galaktyki. W mgławicach planetarnych, gdzie temperatura pyłu wynosi średnio 100 K, jest to dominująca emisja od około 100 GHz.
Widmo promieniowania reliktowego oraz pyłu w przestrzeni międzygwiazdowej:
![\includegraphics[width=7cm]{Rysunki/ism_spectrum_dust.eps}](img546.png)
Bogna Pazderska 2009-01-20