Linie radiowe

Linie spektralne mają określone częstotliwości że względu na przejścia między różnymi dyskretnymi stanami energetycznymi, często związanymi z kwantyzacją orbitalnego i spinowego momentu pędu (angular momentum).

Zawarte w liniach dane:
a) prędkości radialne i wynikające z nich: odległość kosmologiczna, zwykły ruch własny, rotacja, rozkład masy dla galaktyk
b) poszerzenie linii mające charakter: naturalny (związane z zasadą nieoznaczoności, opisane przez profil Lorentza) oraz termiczny (też zapadanie się materii, efekty związane z ciśnieniem)
c) warunki fizyczne jak temperatura, gęstość czy pole magnetyczne (Zeeman effect).

ISM w Galaktyce posiada mniej więcej stałe ciśnienie (ruch masy powyżej prędkości dźwięku redukuje gradient ciśnienia) i różne temperatury i gęstości. Są 4 fazy ISM o porównywalnym ciśnieniu:
(1) zimna (ok. $10~K$) gęste chmury molekularne
(2) chłodna (ok. $10^2~K$) neutralny gaz HI
(3) ciepła (ok. $10^4~K$) zjonizowany gaz HII
(4) gorąca (ok. $10^6~K$) niskiej gęstości zjonizowany gaz (np. bańki utworzone przez SNR)
Wszystkie poza fazą gorącą produkują linie spektralne.

1. Linie rekombinacyjne:

Przejścia między różnymi stanami energetycznymi określonymi główną liczbą kwantową ``n'': $\Delta n =1$ to przejście $\alpha$ np. $H91\alpha$ to przejście między n=92 do n=91
$\Delta n =2$ to przejście $\beta$
$\Delta n =3$ to przejście $\gamma$ itd.

Częstotliwość wyemitowanej linii:

$$\nu = R_M c \left({\frac{1}{n^2} - \frac{1}{(n+\Delta n)^2} }\right)$$

$R_M=R_\infty \left({1+\frac{m_e}{M} }\right)^{-1}$
$R_\infty= 1.09\cdot10^5~cm^{-1}$ - stała Rydberga
$M$ - masa jądra

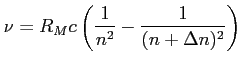
Odległość między kolejnymi przejściami:

$$\frac{\Delta\nu}{\nu} \simeq \frac{3}{n}$$

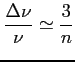
Gaussowki, znormalizowany profil linii związany z samym rozszerzeniem temperaturowym (profil naturalny jest zaniedbywalny):

$$\phi(\nu_0) = \left({\frac{ln2}{\pi} }\right)^{1/2} \frac{2}{\Delta\nu}$$

$$\Delta\nu = \left({\frac{8ln2 k}{c^2} }\right)^{1/2} \left({ \frac{T_e}{M}}\right) ^{1/2} \nu_0$$

$\Delta \nu$ - szerokość połówkowa linii
$\nu_0$ - częstotliwość centrum linii
$T_e$ - temperatura kinetyczna (z rozkładu prędkości Maxwella)
M - masa jądra

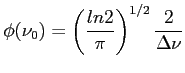
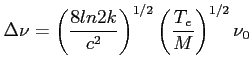
2. Równanie transferu promieniowania
$E_U$ - energia wyższego poziomu energetycznego
$E_L$ - energia niższego poziomu energetycznego
$E=E_U - E_L = h\nu_0$ - energia fotonu wyemitowana przy przejściu
$N_U, N_L$ - ilość atomów czy molekół na danym poziomie energetycznym

$A_{UL}$ - współczynnik Einsteina emisji spontanicznej, p-stwo emisji na jednostkę czasu, $[s^{-1}]$
$B_{UL}$, $B_{LU}$ - współczynniki Einsteina emisji wymuszonej ($B_{UL}$) i absorpcji ($B_{LU}$)
$U_\nu$ - spektralna gęstość energii ( $4\pi B(\nu,T)/c$) $[erg~cm^{-3}~Hz^{-1}]$
$B_{UL}U_\nu$, $B_{LU}U_\nu$ - p-stwo przejścia na jednostkę czasu, $[s^{-1}]$

Wtedy równianie (LTE) dla dwóch poziomów energetycznych, wysokiego (U) i niskiego (L):

$$N_U A_{UL}+N_U B_{UL}U_\nu = N_L B_{LU}U_\nu$$

W czasie przejścia emitowany lub absorbowany jest foton ( $h\nu=E_U-E_L$).  
Współczynniki określone przez równanie Boltzmanna:

$$\frac{N_U}{N_L} = \frac{g_U}{g_L}e^{-\frac{h\nu_0}{kT_E}}$$

$T_E$ - temperatura ekscytacji
$g_U, g_L$ - wagi statystyczne
 
Dla linii 21 cm równanie to wyznacza temperaturę spinową i $N_U, N_L$ określa ilość atomów że spinami równoległymi i antyrównoległymi. Tylko w nielicznych przypadkach jest to temperatura fizyczna.

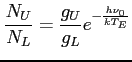
Aby wyznaczyć jakie promieniowanie związane jest z produkcją linii widmowych potrzebne są współczynniki emisji i absorpcji promieniowania:

$$j_\nu = \frac{h\nu_0}{4\pi} A_{UL} N_U \varphi(\nu)$$

$$\alpha_\nu = \frac{h\nu_0}{c}(N_L B_{LU}-N_U B_{UL}) \varphi(\nu)$$

$\nu_0$ - częstotliwość środka linii
$\varphi(\nu)$ - znormalizowany, profil linii, tj.:

$$\int_0^\infty \varphi(\nu) d\nu = 1$$

3. Źródła linii rekombinacyjnych - zjonizowany wodór w przejściach $\Delta n =1$
Temperatura jasnościowa centrum linii (skoro wszystkie znane obszary HII są optycznie cienkie):

$$T_L\simeq T_e \tau_L \simeq 1.92\cdot10^3T_e^{-3/2}EM\Delta\nu^{-1}$$

$\tau_L$ - głębokość optyczna linii
$T_e$ - temperatura elektronowa, $[K]$
$\Delta \nu$ - szerokość połówkowa linii (znormalizowanej), $[kHz]$
$EM$ - miara emisji, $[pc~cm^{-6}]$

$$EM = \int N_e^2 ds$$

$N_e$ - gęstość elektronowa, $[cm^{-3}]$
$s$ - droga przez obłok, $[pc]$

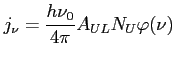
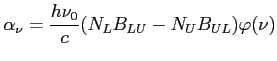
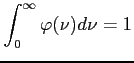
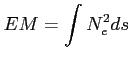
Dla wysokich częstotliwości, gdzie kontinuum swobodno-swobodne też jest optycznie cienkie: stosunek temperatury jasnościowej linii ($T_L$) do temperatury jasnościowej tła ($T_C$):

$$\frac{T_L}{T_C}\simeq 7.0\cdot10^3 \Delta V^{-1} \nu^{1.1} T_e^{-1.15} \left( {1+ \frac{N(He^{+})}{N(H^{+})}} \right) ^{-1}$$

$\Delta V$ - szerokość linii wyrażona w prędkościach radialnych, $[km/s]$
$\nu$ - częstotliwość, $[GHz]$
$T_e$ - temperatura elektronowa, $[K]$
$N(He^{+})/N(H^{+})$ - stosunek ilości, typowo 0.08 ($He^{+}$ odnosi się do continuum)

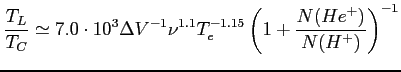
W radioastronomii mierzy się częstotliwości stąd prędkość radialną wyraża się przy ich użyciu (w astronomii optycznej używa się długości fal i przy ich użyciu liczy się tą prędkość, zaś obie wyliczone prędkości nie są sobie dokładnie równe):

$$\frac{V_r}{c} = \frac{\nu_s-\nu_o}{\nu_s}$$

$\nu_s$ - częstotliwość wysłana, pierwotna
$\nu_o$ - częstotliwość obserwowana

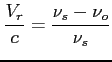
4. Linie molekularne
Molekuły:

a)

polarne - ma niezerowy stały elektryczny moment dipolowy

b)

homonuklearne (generalnie symetryczne molekuły) - bez stałego elektrycznego momentu dipolowego np. $H_2$

Jeśli obiekt ma linie pola charakterystyczne dla dipola elektrycznego (np. 2 różnoimienne ładunki) to jest dipolem i posiada dipolowy moment elektryczny. Zaś moc wypromieniowana przy przejściu zależy od momentu dipolowego.

Zależność współczynnika Einsteina związanego z emisją spontaniczną:

$$A_{UL}=\frac{64\pi^4}{3hc^3} \nu_{UL}^3 \vert\mu_{UL}\vert^2$$

gdzie:

$$\vert\mu_{J+1->J}\vert^2 = \frac{\mu^2 (J+1)}{2J+3}$$

$\mu$ - średni dipolowy elektryczny moment dipolowy

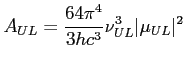
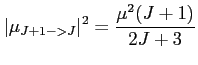
Częstotliwości emisji są zależne od momentu pędu:

$$L=n\hbar = n h/(2\pi) = J(J+1) \hbar$$

$n$ - główna liczba kwantowa
$J$ - liczba kwantowa związana z momentem pędu

Przypadek dwuatomowy dla mas $m_A$, $m_B$ znajdujących się w odległości $r_e$ np. $H_2$, $CO$:

$$L=mr_e^2\omega$$

Gdzie ``m'' zredukowana masa:

$$m = \frac{m_Am_B}{m_A+m_B}$$

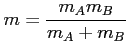
Generalnie linie rotacyjne (energie rotacji też są skwantowane i zachodzi zmiana liczby kwantowej J), gdzie energia rotacji:

$$E_{rot}=I \omega^2 / 2 = \hbar^2 J (J+1) / (2mr_e^2)$$

$I$ - moment bezwładności

Przejścia dozwolone:

$$\Delta J = \pm 1$$

Wyemitowana częstotliwość podczas przejścia:

$$\nu = \frac{\hbar J}{2\pi mr_e^2}$$

$J=1,2,...$ - początkowa liczba kwantowa

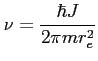
Minimalna temperatura gazu (kinetyczna) potrzebna do znaczącej ekscytacji zderzeniowej (z energii zderzeniowej i kinetycznej):

$$T_{min} \simeq \frac{\nu h (J+1)}{2k}$$

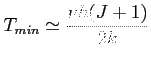
5. Linia 21 cm

Molekuła $H_2$ jest symetryczną molekułą, bez stałego magnetycznego momentu dipolowego stąd nie emituje dających się odkryć linii spektralnych na częstotliwości radiowej. Ale emituje linię nadsubtelną 21 cm tj. 1420.4 MHz. Radioteleskopem dokonuje się pomiarów temperatury antenowej, którą potem przelicza się na temperaturę jasnościową.

Dla linii 21 cm współczynnik emisji spontanicznej wynosi:

$$A_{10} \simeq 2.86~10^{-15}~s^{-1}$$

Stąd połowiczny czas życia przejścia (czas po którym połowa atomów przejdzie na niższy poziom energetyczny wynosi 11 mln lat):

$$\tau_{1/2} = A^{-1}_{10} = 3.5\cdot10^{14}~s = 11~mln~lat$$

Jeśli średni czas między zderzeniami jest o wiele krótszy niż $\tau_{1/2}$ to mamy LTE (grubość optyczna » 1, częste zderzenia) i temperatura ekscytacji z prawa Boltzmanna (tu: spinowa $T_s$) jest równa temperaturze kinetycznej.
 
``Klasyczna'' wartość temperatury spinowej $T_s=125~K$

a) Gęstość kolumnowa
Zdefiniowana jest jako (ilość pierwiastka jest proporcjonalna do gęstości kolumnowej):

$$\eta = \int N(s) ds$$

$N(s)$ - ilość danego atomu w jednostce objętości, $[cm^{-3}]$
$s$ - droga w chmurze (cała droga do chmury, ale obszary o małej gęstość HI można zaniedbać), $[cm]$

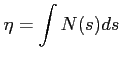
Związek z temperaturą spinową:

$$\eta_H \simeq 1.8224\cdot10^{18}~T_S \int_{linia} \tau(V) dV$$

$V$ - prędkość radialna w danym punkcie linii, $[km/s]$
$\tau$ - głębokość optyczna

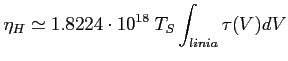
Ogólny związek temperatury jasnościowej i spinowej:

$$T_b = T_c e^{-\tau(V)} + T_s \left( {1-e^{-\tau(V)}}\right)$$

$T_s$ - temperatura spinowa
$T_c$ - temperatura jasnościowa tła (W większości przypadków = 0)

Ponieważ większość obszarów HI jest optycznie cienka to można przyjąć, że:

$$T_b(V)=T_s\tau(V)$$

I wtedy otrzymamy wzór na gęstość kolumnową:

$$\eta_H \simeq 1.8224\cdot10^{18}~\int_{linia} T_b(V) dV$$

$T_b$ - temperatura jasnościowa linii, $[K]$
$V$ - prędkość radialna w danym punkcie linii, $[km/s]$

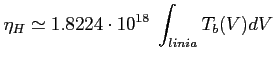
b) Masy:
Dla obszaru optycznie cienkiego tj. ($\tau<<1$) całkowita masa neutralnego wodoru wynosi:

$$\frac{M_H}{M_\odot} \simeq 2.36\cdot10^5 D^2 \int S(V) dV$$

$D$ - odległość do obiektu (np. z prawa Hubble'a), $[Mpc]$
$S(V)$ - strumień w funkcji prędkości, $[Jy]$
$V$ - prędkość radialna, $[km/s]$

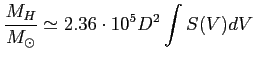
Całkowitą masę można obliczyć z przyrównania siły grawitacji do siły dośrodkowej co daje przy założeniu sferycznego rozkładu masy:

$$\frac{M}{M_\odot} \simeq 2.3\cdot10^5 (V_r/sin(i))^{-2}r$$

Inklinacja:

$$cos(i) \approx \frac{\theta_m}{\theta_M}$$

$\theta_m$ - rozmiar kątowy mniejszej osi
$\theta_M$ - rozmiar kątowy większej osi
$V_r$ - prędkość radialna środka linii, $[km/s]$
$r=\theta_{1/2}D$ - promień źródła, $[kpc]$
$D$ - odległość, $[kpc]$

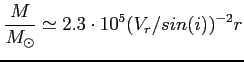
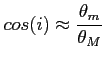
Efekt Zeemana powoduje rozczepienie poziomów energetycznych (w próżni poziomy energii w atomie są niezależne od kierunku momentu pędu, jednak w obecności pola magnetycznego ta zależność powstaje, czego wynikiem jest rozdzielenie obu polaryzacji kołowych) i odległość między tymi liniami dla linii 21 cm wynosi:

$$\Delta\nu_{\small Z} = 2.8\cdot10^6B$$

$B$ - pole magnetyczne, $[G]$
np. przeciętne pole magnetyczne w obłokach wynosi $2\cdot10^{-5}~G$ co oznacza rozczepienie rzędu 50 Hz.

Od razu daje całe, regularne pole magnetyczne (emisja synchrotronowa i efekt Faradaya tylko jedną składową). Zmierzone dotychczas dla linii 21 cm (wodór) i 18 cm (OH), lecz niestety, za względu na słabość efektu, jego obserwacje są ograniczone do naszej Galaktyki.