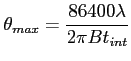Interferometr ma pewne pole widzenia (Total FoV) zdefiniowane przez rozmiar pierwszej wiązki (primery beam). jednakże różnego rodzaju aberracje zmniejszają użyteczne pole, choć dla różnych rodzaju obserwacji, różne aberracje mogą być najbardziej istotne.
1. Mapowanie w 3 wymiarach (''3-D sky`` effect)
Współrzędne (u,v) są współrzędnymi przestrzennymi zdolnymi do opisu źródła w 2 wymiarach (rzut sfery niebieskiej na płaszczyznę). Dla większych odległości od osi (punktu na który patrzy radioteleskop) zakrzywienie sfery niebieskiej jest już istotne i potrzebny jest pełny układu współrzędnych (u,v,w). Wtedy konieczne jest zastosowania pełnego wyrażenia:
Jednakże kiedy ograniczymy naszą mapę do małego obszaru na niebie możemy zastosować przybliżenie w którym używamy tylko współrzędnych (u,v). Warunek na zastosowanie tego przybliżenia można zapisać w postaci:
lub (pole widzenia że względu na krzywiznę nieba)
B - rzut bazy na kierunek przychodzącej fali
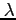 - długość fali (im dłuższa fala tym mniejszy kąt, gdzie przybliżenie jest dobre)
- długość fali (im dłuższa fala tym mniejszy kąt, gdzie przybliżenie jest dobre)
W astronomii optycznej odpowiada to zjawisku aberracji sferycznej.
2. Efekt pasma częstotliwości (bandwidth smearing):
Jeśli uwzględnimy to, że interferometr odbiera w skończonym paśmie częstotliwości to otrzymamy:
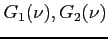 - funkcja opisująca zmiany amplitudy i fazy w paśmie częstotliwości dla obu anten
- funkcja opisująca zmiany amplitudy i fazy w paśmie częstotliwości dla obu anten
Jeśli założymy, że 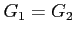 - jest prostokątną funkcją w paśmie
- jest prostokątną funkcją w paśmie
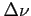 to otrzymamy:
to otrzymamy:
gdzie:
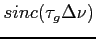 - funkcja obwiedni (fringe-washing function)
- funkcja obwiedni (fringe-washing function)
Jak widać skończone pasmo przepuszczania powoduje utratę koherencji na dużych kątach, bo amplituda obwiedni zostaje zredukowana.
Tłumienie jest małe jeśli:
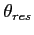 - zdolność rozdzielcza interferometru (proporcjonalna do
- zdolność rozdzielcza interferometru (proporcjonalna do 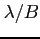 )
)
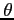 - kąt mierzony od centrum pola
- kąt mierzony od centrum pola
Stąd drugie ograniczenie pola widzenia, teraz że względu na przedział częstotliwości (bandwidth smearing):
Zatem straty są duże przy obserwacji dużych obiektów w szerokich pasmach. Dlatego generalnie stosuje się systemy wielopasmowych, wąskich kanałów (choć jest to droższe rozwiązanie).
Pasmo i funkcję widzialności prezentuje rysunek:
Efekt ten rośnie radialnie wraz z oddalaniem się od środka fazy i generalnie stanowi największe ograniczenie. W astronomii optycznej odpowiada to zjawisku aberracji chromatycznej.
3. Ograniczenie na czas integracji (integration time smearing):
Istnieje jeszcze trzecie ograniczenie na pole widzenia, związane z czasem integracji. Interferometr zbierający dane z jednego punktu na niebie uśrednia otrzymany sygnał, a zatem też fazę stąd ważne jest by owa faza nie zmieniła się znacząco w czasie integracji. Na zmianę fazy znacząco wpływa zmieniające się raz z ruchem położenie listków bocznych czy zmienna atmosfera. Przybliżony wzór dla idealnej pogody, mówi że:
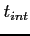 - czas integracji,
- czas integracji, ![$ [s]$](img512.png)
Ale przy dokładnym planowaniu obserwacji należy uwzględnić podawane dla danego instrumentu wartości. Efekt ten jest stały dla elips usytuowanych wokół środka pola, także nie rośnie dokladnie radialnie.
Bogna Pazderska
2009-01-20
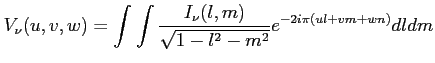
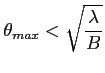
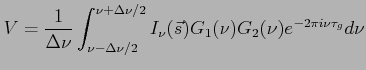
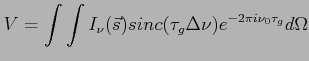
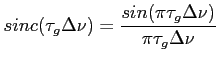
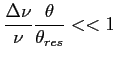
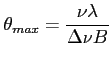
![\includegraphics[width=6cm]{Interferometr/delay_pattern.eps}](img509.png)