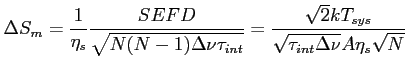Next: Baza, a rozdzielczość i Up: Interferometria Previous: Aberracja apertury Spis rzeczy
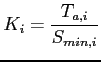
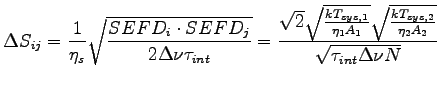
![]() - efektywność anteny pierwszej, drugiej i obu
- efektywność anteny pierwszej, drugiej i obu
![]() - temperatura systemowa danej anteny
- temperatura systemowa danej anteny
![]() - czas integracji
- czas integracji
![]() - ilość baz (dla 2 anten N=1)
- ilość baz (dla 2 anten N=1)
![]() - przedział częstotliwości
- przedział częstotliwości
![]() - opertury poszczególnych anten
- opertury poszczególnych anten
Czułość interferometru złożonego z N identycznych anten, o tym samym
![]() ,
, ![]() i
i ![]() wyraża się wzorem:
wyraża się wzorem: