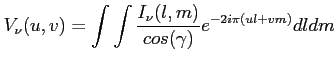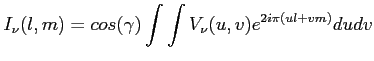Mając obie składowe odpowiedzi radioteleskopu można je połączyć w jedną uzyskując funkcję widzialności:
gdzie amplituda i faza fali:
co daje:
Funkcję widzialności (ciemna zieleń) wraz z funkcją jasności 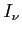 (czarny) i listkami (czerwień) przedstawia poniższy rysunek. Górna część dotyczy dużej odległości między antenami (b), zaś cześć dolna małej odległości (małej bazy).
Można teraz wyznaczyć poszczególne wielkości w funkcji kątów (direction cosines):
(czarny) i listkami (czerwień) przedstawia poniższy rysunek. Górna część dotyczy dużej odległości między antenami (b), zaś cześć dolna małej odległości (małej bazy).
Można teraz wyznaczyć poszczególne wielkości w funkcji kątów (direction cosines):
A także zastąpić kierunek 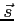 przez jego składowe:
przez jego składowe:
Co pozwala zapisać kąt bryłowy źródła jako:
Zapisując wektor bazy przy pomocy współrzędnych apertury (u,v,w) otrzymamy:
Co po podstawieniu do funkcji widzialności daje:
Jest to 2-wymiarowa transformata Fouriera z funkcji jasności. Przekształcając to równanie by uzyskać szukaną funkcję jasności źródła otrzymamy:
Skoro w tym funkcja widzialności jest transformatą Fouriera z funkcji jasności, a ta z kolei funkcja jest rzeczywista (część urojona równa się zero) to V(u,v) musi być macierzą hermitowską tj.
A zatem wystarczy znać połowę tej funkcji tj. obserwować źródło przez 12h by w pełni odtworzyć obraz.
Problem fazy:
Mierzona przez interferometr faza jest zniekształcona na skutek wpływu atmosfery czy nierówności chodu zegara atomowego. Dlatego stosuje się specjalną technikę jej odzyskiwania zwaną metodą zamkniętych faz. Jeśli dysponujemy trzema antenami to faza listków interferencyjnych jest równa różnicy faz sygnałów odbieranych na poszczególnych antenach. Stąd suma trzech faz w zamkniętym trójkącie baz dla źródła punktowego powinna więc być równa zero. I przez porównywanie modelu z obserwacjami przez kilka iteracji można odzyskać prawdziwy wygląd nieba. Im więcej baz ( N(N-1)/2 <- ilość baz, gdzie N - liczba anten) tym więcej zamkniętych trójkątów, a zatem pełniejsza informacja.
Bogna Pazderska
2009-01-20
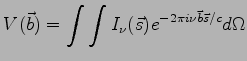
![\includegraphics[width=10cm]{Interferometr/visibility.eps}](img480.png)
![\includegraphics[width=6cm]{Interferometr/uwv_wsp.eps}](img487.png)