Rozważmy promieniowanie pochodzące z kierunku 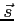 z kąta
z kąta 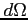 odbierane w wąskim paśmie częstotliwości przez układ 2 anten. Wtedy na pierwszej antenie dostaniemy napięcie:
odbierane w wąskim paśmie częstotliwości przez układ 2 anten. Wtedy na pierwszej antenie dostaniemy napięcie:
Aby na drugiej antenie odebrać promieniowanie wysłane w tej samej chwili czasu trzeba uwzględnić różnicę w czasie dotarcia fali do obu anten. Jeśli 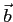 to wektor odległości między antenami (baseline), zaś
to wektor odległości między antenami (baseline), zaś 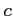 - prędkość fali e-m w próżni to różnica w czasach przyjścia wynosi:
- prędkość fali e-m w próżni to różnica w czasach przyjścia wynosi:
Zatem na drugiej antenie otrzymamy odbierane napięcie:
Po wymnożeniu obu sygnałów w mikserze:
Po uśrednieniu sygnału w czasie otrzymamy:
Zatem średni sygnał jest niezależny od czasu, ale zależny od opóźnienia.
Odpowiedz anteny dla źródła rozciągłego można zapisać wzorem:
Odpowiednie wymnożenie sygnałów z obu odbiorników (cross-correlation) powoduje, że sygnały obecne tylko w jednym odbiorniku (a zatem zakłócenia) nie będą obecne w wyjściu interferometru, co pozwala na prowadzenie o wiele czulszych obserwacji. Funkcja ta bowiem daje największe bezwzględne wartości, gdy sygnały w danej chwili czasu są do siebie najbardziej podobne, zaś najbliższe zera, gdy się od siebie różnią
Zależność od jasności źródła:
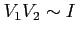 . Wielkość otrzymywanego sygnału (współczynnik proporcjonalności) jest też zależna od apertury anteny i wzmocnienia systemu, ale tych parametrów nie wyznacza się bezpośrednio tylko dokonuje kalibracji.
. Wielkość otrzymywanego sygnału (współczynnik proporcjonalności) jest też zależna od apertury anteny i wzmocnienia systemu, ale tych parametrów nie wyznacza się bezpośrednio tylko dokonuje kalibracji.
Stąd odpowiedz radioteleskopu można zapisać jako:
Sygnał wysyłany przez źródło można rozpisać jako sumę symetrycznej i antysymetrycznej części. Zaś cosinus jest funkcją symetryczną, a całka z iloczynu funkcji symetrycznej i antysymetrycznej jest równa zero, stąd takie wyrażenie było by wrażliwe tylko na część sygnału wysyłanego że źródła. Aby odebrać część antysymetryczną należy użyć funkcji sinus (antysymetrycznej) co robi się przez zastosowanie w układzie odbiorczym przesuwnika fazy o 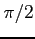 . Zamiast przesunięcia fazowego można też używać zapóźnienia w czasie.
. Zamiast przesunięcia fazowego można też używać zapóźnienia w czasie.
Wtedy po wymnożeniu sygnałów i przesunięciu fazy o 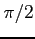 mamy sygnał:
mamy sygnał:
Zaś po uśrednieniu:
Co po pocałkowaniu po źródle daje:
Zaś po wykalibrowaniu (uwzględnieniu wzmocnienia np. przez porównanie z źródłem o znanym strumieniu) dostajemy:
Wyjście z interferometru posiada zatem na przemian wiązkę dodatnią i ujemną (kolejne ekstrema np. funkcji sinus). Kolejne maksimum następuje dla kąta (fringe spacing):
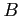 - rzut bazy na kierunek przychodzącej fali
- rzut bazy na kierunek przychodzącej fali
To daje ograniczenie na wielkość obserwowanych obiektów. Jeżeli rozmiar radioźródła jest większy od odległości dodatniej i ujemnej wiązki to sygnał zacznie się zerować (resolved source). A zatem np. usunąć wpływ Galaktyki z danych. (Przy zmiennej bazie pozwala to w prosty sposób wyznaczyć rozmiar radioźródła, jako że sygnał powinien zacząć maleć, gdy rozmiar
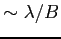 .) Poniżej rysunek przedstawia obserwacje źródła przy krótkiej (lewa część) i długiej (prawa część) bazie.
.) Poniżej rysunek przedstawia obserwacje źródła przy krótkiej (lewa część) i długiej (prawa część) bazie.
Bogna Pazderska
2009-01-20
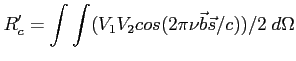
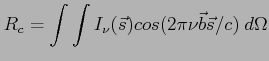
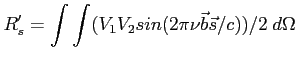
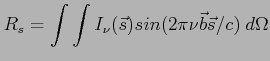
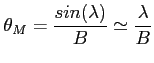
![\includegraphics[width=4cm]{Interferometr/shortbaseline.eps}](img473.png)
![\includegraphics[width=4cm]{Interferometr/longbaseline.eps}](img474.png)