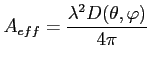Jednak podstawową wielkością opisującą antenę jest jej apertura (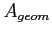 ) i apertura efektywna definiowana jako:
) i apertura efektywna definiowana jako:
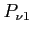 - odbierana moc spektralna w danej polaryzacji [
- odbierana moc spektralna w danej polaryzacji [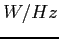 ]
]
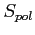 - gęstość strumienia w odbieranej polaryzacji [
- gęstość strumienia w odbieranej polaryzacji [
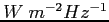 ]
]
Dla źródła niespolaryzowanego
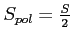
Ponieważ odbiorniki generalnie odbierają polaryzację kołową, a pojedyncza antena nie obserwuje pojedynczych źródeł o takiej polaryzacji np. masera to stosuje się to do większości obserwacji.
Dla bezstratnej anteny można ją też wyrazić wzorem, wiążącym ją z kierunkowością:
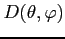 - wzmocnienie, kierunkowość
- wzmocnienie, kierunkowość
Wniosek: Im krótsza długość fali tym potrzebna jest większa antena. Dlatego tylko dla fal większych niż około 1 m korzysta się z anten dipolowych. Stąd generalnie łatwiej obserwować na dłuższych falach (większa apertura efektywna, rozdzielczość, mniejsza wymagana dokładność czaszy), ale do pewnej wielkości granicznej, powyżej której fala ``nie zauważy'' anteny (zależna od średnicy falowody, zazwyczaj średnica oświetlacz wynosi ok. 8 razy długość fali).
Bogna Pazderska
2009-01-20
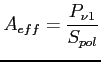
![]()