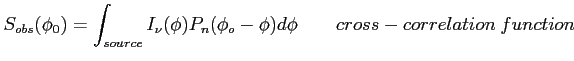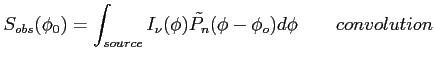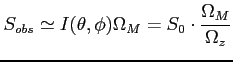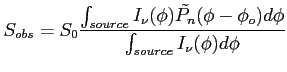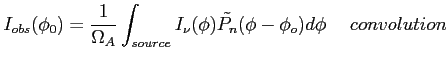Wielkości mierzone różnią się od wielkości prawdziwych, ze względu na właściwiości odbiorcze anteny, które różnią się w zależności od kierunku (opisywane są one przez charakterystykę kierunkową mocy). Stąd obserwowana gęstość strumienia:
Zaniedbując 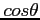 i biorąc przypadek anteny posiadającej symetrię sferyczną (jak antena paraboliczna):
i biorąc przypadek anteny posiadającej symetrię sferyczną (jak antena paraboliczna):
Gdzie
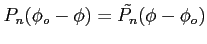
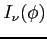 - liniowa jasność źródła (wielkość ``mierzona'' przy skanowaniu źródła)
- liniowa jasność źródła (wielkość ``mierzona'' przy skanowaniu źródła)
- a)
- Przybliżenie dla małego źródła:
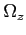 - rozmiar kątowy źródła
- rozmiar kątowy źródła
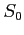 - gęstość strumienia źródła
- gęstość strumienia źródła
- b)
- Dla źródła rozciągłego, o rozmiarach o wiele większych niż szerokość listka głównego:
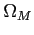 - kąt bryłowy listka głównego (main beam solid angle)
- kąt bryłowy listka głównego (main beam solid angle)
Dla wiązki głównej opisanej rozkładem Gaussa:
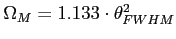
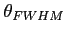 - szerokość wiązki na połowie mocy
- szerokość wiązki na połowie mocy
- c)
- Dla źródła o rozmiarach zbliżonych do rozmiaru wiązki:
Jasność obserwowana:
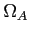 - pełna szerokość wiązki
- pełna szerokość wiązki
Stąd dla źródeł rozciągłych podaje się wielkości w 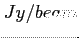 przy podaniu wielkości wiązki (rozmiary listka głównego). Teoretycznie można dokonać dekonwolucji wiązki, jednakże się tego nie robi ze względu na to, że wymaga ona dodatkowych założeń (np. informacji o rozmiarze źródła), a zatem nie jest ona jednoznaczna. Natomiast w przypadku interferometri, gdzie charakterystyka kierunkowa interferometru jest skomplikowana i nie do opisania przez pojedyńczą wiązkę dokonuje się ``czyszczenie obrazu'', które polega na uzyskaniu takiego obrazu, jakby interferometr miał charakterystykę mocy opisaną przez prostego Gaussa, a zatem min. na konwolucji z czystą wiązką.
przy podaniu wielkości wiązki (rozmiary listka głównego). Teoretycznie można dokonać dekonwolucji wiązki, jednakże się tego nie robi ze względu na to, że wymaga ona dodatkowych założeń (np. informacji o rozmiarze źródła), a zatem nie jest ona jednoznaczna. Natomiast w przypadku interferometri, gdzie charakterystyka kierunkowa interferometru jest skomplikowana i nie do opisania przez pojedyńczą wiązkę dokonuje się ``czyszczenie obrazu'', które polega na uzyskaniu takiego obrazu, jakby interferometr miał charakterystykę mocy opisaną przez prostego Gaussa, a zatem min. na konwolucji z czystą wiązką.
Bogna Pazderska
2009-01-20
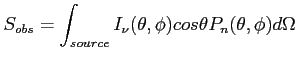
![]() i biorąc przypadek anteny posiadającej symetrię sferyczną (jak antena paraboliczna):
i biorąc przypadek anteny posiadającej symetrię sferyczną (jak antena paraboliczna):