Definicja

Def. (Widmowa) gęstość strumienia (często używa się tylko strumień) (flux density) to moc odebrana w przedziale częstotliwości przez daną powierzchnię, prostopadłą do kierunku na źródło:

$$S_\nu =\frac{dP}{A d\nu} = \int_{source} I_\nu (\theta, \phi) cos\theta d\Omega$$

Jednostka SI: $[W~m^{-2}Hz^{-1}]$
Jednostka cgs: $[erg~cm^{-2}]$
$1~Janski = 1~Jy = 10^{-26}~W~m^{-2}Hz^{-1}=10^{-23}~erg~cm^{-2}$ $1~solar~unit = 1~su = 10^{-22}~W~m^{-2}Hz^{-1}=10^{-19}~erg~cm^{-2}$
 
$P$ - moc odebrana (liczona na obie polaryzacje)
$A$ - powierzchnia zbierająca (dokładniej: efektywna powierzchnia)

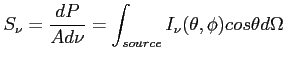
Dla źródła punktowego, izotropowego:
$P_e$ - moc emitowana przez źródło
$A_s=4\pi r^2$ - powierzchnia sfery odległej o ``r'' od źródła, na którą pada moc $P_e$

np: dla źródła o $S=1\,Jy$, sygnał odebrany przez 32 m radioteleskop o efektywności 60% ( $A_{eff}=60\% \,\pi \,(16\,m)^2 = 483\,m^2$) wynosi $4.8\cdot10^{-24}\,W\,Hz^{-1}$ w obu polaryzacjach, co w paśmie $\Delta\nu=10\,MHz$ daje moc odebraną $P_{o} = 4.8\cdot10^{-17}\,W$. Jeśli źródło jest izotropowe i znajduje się w odległości $r=1\,AU$ to emituje ono moc $P_{w} = P_{o}\cdot 4\pi r^2/A_{eff} = 3\cdot10^4\,W$.

Ale jeśli źródło niewielkie (duże są np. Obłoki Magellana) $\Omega<<1~rad$ to $cos\theta \simeq 1$ i:

$$S_\nu = \int_{source}I_\nu (\theta, \phi) d\Omega$$

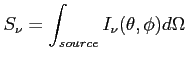
Dla dyskretnego źródła (punktowe i rozciągłe) lub stałej jasności:

$$S_\nu \simeq I_\nu \Omega \simeq I_\nu \frac{\pi r^2}{D^2}$$

$d \Omega = sin\theta d\theta d\phi$
$\Omega \simeq \frac{1}{4}\pi \Theta^2$ - rozmiar kątowy źródła w przybliżeniu małego kąta, $[sr]$
$\Theta$ - średnica kątowa źródła, $[ra]$
$r$ - promień źródła
$D$ - odległość do źródła

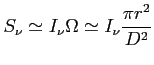
Wnioski:

- natężenie (lub jasność powierzchniowa) nie zależy od odległości
- gęstość strumienia zależy od odległości!

- strumień mierzymy dla źródeł dyskretnych
- dla rozciągłych mierzona jasność, zaś gęstość strumienia jest obliczana

np: Na radiowym niebie obłoki gazu międzygwiazdowego o temperaturze $10\div100~K$, ale o rozmiarach kątowych rzędu arcmin, mogą być dużo silniejsze niż odległe gwiazdy o $10^3\div10^4~K$.

Związek z wrażeniami wzrokowymi: 2 razy jaśniej to różnica o 1 magnitudo, a zatem wzrost strumienia o 2.5.

$$1=m_1-m_2=-2.5log\left({\frac{F_1}{F_2}}\right) = -2.5log\left({\frac{S_1}{S_2}}\right)$$

$F_1$, $F_2$ - strumienie promieniowania, $[W~Hz^{-1}], [erg]$
$S_1$, $S_2$ - gęstości strumienia, $[W~m^{-2}Hz^{-1}], [erg~cm^{-2}]$