Next: Bibliografia Up: radioastronomia Previous: Gromady galaktyk Spis rzeczy
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Masa Ziemi:
|
| Masa Słońca:
|
| Promień Ziemi:
|
| Promień Słońca:
|
| Odległość Ziemia - Słońce:
|
| Bolometryczna dzielność promieniowania Słońca:
|
| Rok:
|
| NAZWA STAŁEJ | SYMBOL | Układ SI | UKŁAD CGS |
|---|---|---|---|
| Stała Plancka |
|
|
|
| Prędkość światła w próżni |
|
|
|
| Impedancja charakt. próżni |
|
|
|
| Stała grawitacji |
|
|
|
| Ładunek elementarny |
|
|
|
| Masa elektronu |
|
|
|
| Stała Boltzmanna |
|
|
|
| Stała Stefan-Boltzmanna |
|
|
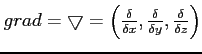
![]()
![]()
Twierdzenie Ostrogradzkiego-Gaussa:
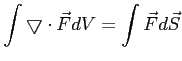
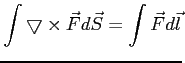
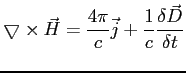
Bogna Pazderska 2009-01-20