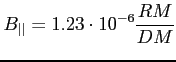Rotacja Faradaja

Rotacja Faradaja - efekt związany z oddziaływaniem spolaryzowanego światła z polem magnetycznym, powodujący zmianę kąta polaryzacji liniowej. W przestrzeni międzygwiazdowej związany z swobodnymi elektronami, które mają inny współczynnik załamania $(n= c/V_o)$ dla różnych polaryzacji kołowych. Zależność współczynnika załamania od częstości cyklotronowej elektronu:

$$n=\sqrt{1-\frac{\nu_p^2}{\nu (\nu\pm \nu_B)}}$$

$\nu_B$ - częstotliwość gyroskopowa

$$\nu_B=\frac{eB}{2\pi mc}$$

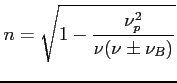
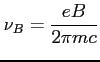
Wynikiem jest skręcenie wektora magnetycznego. Kąt rotacji (tu polaryzacji liniowej) wynosi:

$$\beta = RM \lambda^2$$

Dla ISM czynnik RM (miara rotacji) wyraża się wzorem:
(UKŁAD JEDNOSTEK SI):

$$RM = \frac{e^3}{8\pi^2 \varepsilon_0 m_e^2 c^3} \int_0^d n_eB_{\vert\vert}ds = 2.62\cdot10^{-13}~\int_0^d n_e B_{\vert\vert}ds$$

Jednostka: $[rad/m^2]$
$B_{\vert\vert}=Bcos\alpha$ - pole magnetyczne (składowa radialna), $[T]$
$d$ - cała droga przebyta w danym ośrodku, $[m]$
$n_e$ - gęstość elektronowa, $[1/m^3]$

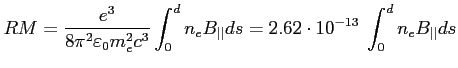
(UKŁAD JEDNOSTEK CGS):

$$RM = \frac{e^3}{2\pi m_e^2 c^4} \int_0^d n_eB_{\vert\vert}ds$$

Jednostka: $[rad/cm^2]$
$B_{\vert\vert}$ - pole magnetyczne (składowa radialna), $[G]$
$d$ - cała droga przebyta w danym ośrodku, $[cm]$
$e$ - ładunek elementarny, $[esu]$
$n_e$ - gęstość elektronowa, $[1/cm^3]$
 
Jak $RM>0$ to pole zwrócone do nas. W skład mierzonej wartości wchodzi np. RM od Galaktyki, źródła i ISM. Dodatkowym problemem jest degeneracja kąta skręcenia tj. $\beta =\beta_0 \pm n\pi$.

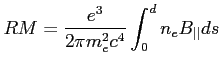
Pozwala to przy spolaryzowanej emisji (jak synchrotronowa) określić gęstość elektronową i przy danych o polaryzacji dla min. 2 długości fal: składową radialną pola magnetycznego. Efekt rośnie z długością fali (zazwyczaj istotny dla fal dłuższych niż kilka centymetrów) i dla źródeł rozciągłych prowadzi do spadku polaryzacji (ISM też ma pewne pole magnetyczne).
 
Jednoczesna znajomość z obserwacji miary rotacji i dyspersji (co jest możliwe przy obserwacji pulsarów) tj. RM i DM pozwala bez żadnych dodatkowych założeń (np. dotyczących gęstości elektronowej) wyznaczyć wartość składowej radialnej pola magnetycznego (wyrażona w Gaussach) dla ISM:

$$B_{\vert\vert}=1.23\cdot10^{-6}\frac{RM}{DM}$$

 
Uzyskane wartości składowej $B_{\vert\vert}$ dla ISM są w zakresie od $0.3~\mu G$ do $3~\mu G$.