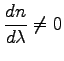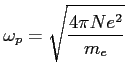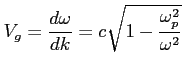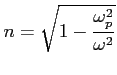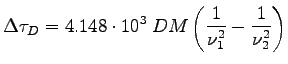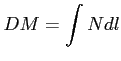Dyspersja fal radiowych

Dyspersja fal radiowych oznacza, ze:

$$\frac{dn}{d\lambda}\neq 0$$

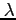$\lambda$ - długość fali
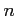$n$ - współczynnik załamania, wyrażony wzorem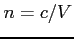 $n=c/V$
 
Większość Wszechświata składa się z plazmy (począwszy od okresu ponownej rejonizacji Wszechświata), którą w najprostszy sposób można opisać jako cienki ośrodek złożony z równomiernie rozłożony jonów i wolnych elektronów, tak że całkowity ładunek równa się zero. Taki ośrodek drga z częstością zwaną częstością własną plazmy:

$$\omega_p=\sqrt{\frac{4\pi Ne^2}{m_e}}$$

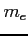$m_e$ - masa elektronu
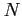$N$ - gęstość elektronowa, $[cm^{-3}]$
 
Zależność prędkości grupowej (prędkość propagacji paczki falowej, nie pojedynczej fali e-m) od częstotliwości fali 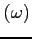$(\omega)$ i plazmy $(\omega_p)$:

$$V_g=\frac{d\omega}{dk}=c\sqrt{1-\frac{\omega_p^2}{\omega^2}}$$

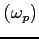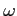$\omega$ - częstość kołowa paczki falowej
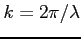$k=2\pi/\lambda$ - liczba falowa
 
Zatem widać, że fala e-m może przejść przez ośrodek tylko wtedy, gdy 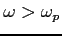$\omega >\omega_p$, bo tylko wtedy 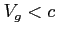$V_g<c$. Jest to główną przyczyną dla której nie możemy obserwować zbyt długich fal radiowych (częstotliwości mniejsze od częstotliwości własnej jonosfery).
 
Teraz można zapisać współczynnik załamania w funkcji obu częstości:

$$n=\sqrt{1-\frac{\omega_p^2}{\omega^2}}$$

 
Druga konsekwencja dyspersji jest wydłużenia się czasu przyjścia pulsu radiowego z częstotliwością. Ale jednocześnie pozwala to (służą temu obserwacje pulsarów) poznać własności ośrodka międzygwiazdowego. Różnica między czasami przyjścia dwóch pulsów (w 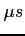$\mu s$) na dwóch różnych częstotliwościach wyraża się wzorem:

$$\Delta\tau_D = 4.148\cdot10^3~DM\left( {\frac{1}{\nu_1^2}-\frac{1}{\nu_2^2}}\right)$$

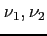$\nu_1, \nu_2$ - częstotliwości, $[MHz]$
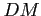$DM$ - miara dyspersji, $[cm^{-3}pc]$
 
Gdzie miara dyspersji jest zdefiniowana jako:

$$DM=\int N dl$$

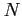$N$ - gęstość elektronów, $[cm^{-3}]$
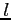$l$ - odległość (długość obszaru, gdzie nastepuje dyspersja), $[pc]$
 
Zatem poznanie różnicy czasów przyjścia pulsów pozwala wyznaczyć miarę dyspersji, która przy znanej odległości daje możliwość oszacowania średniej gęstości elektronowej.