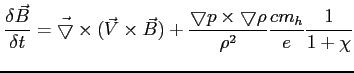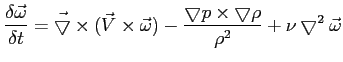Kosmologiczne pole magnetyczne

1. PMF (premodrial magnetic field):

- fluktuacje gęstości potrafią wytłumaczyć mniejsze multipole, natomiast wciąż pozostaje problem kątowego widma mocy dla większych kątów.
- wyższe multipola mogą zostać wytłumaczone jeśli doda się pierwotne pole magnetyczne
- Ograniczenia na pierwotne pole wynikające min. z widma mocy (praca Yamazaki, Ichiki i inni):

$$1~nG < \vert B_\lambda \vert< 4.7~nG$$

Po wzmocnieniu tłumaczą one obserwowane pola magnetyczne w galaktykach i gromadach galaktyk (obserwowane pole $0.1-1\mu G$).
 
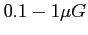Przed rekombinacją PMF mogło już mieć wpływ na zachowanie Wszechświata. Wiąże się to z tym, że Wszechświat wypełniała plazma, więc dominowały zjawiska z nią związane, z czego między 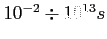$10^{-2}\div10^{13}s$ panowała przewaga sił e-m nad grawitacyjnymi:

• w czasie inflacji: ekspansja wzdłuż linii pola rozciąga linie pola i oddziaływuje przeciw naprężeniu magnetycznemu, zaś ekspansja prostopadła do liń pola jest wspomagana przez ciśnienie magnetyczne. Stąd Wszechświat rozszerza się wolniej wzdłuż kierunku pola, a zatem redshift obiektów w tym kierunku jest zredukowany w stosunku do redshiftu przy $\vec{B}=\vec{0}$.
  
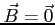• w czasie nukleosyntezy: wzrost gęstości pola magnetycznego powoduje wzrost tempa ekspansji (bo pole wpływa na gęstość elektornów, co wpływa na ilość neutronów), ale jednocześnie powoduje wzrost tempa ekspansji (mniej czasu na reakcje). Jednak pierwszy efekt jest silniejszy zatem wypadkowo powoduje to wzrost obfitości $~^4He$.

 
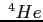Jednak te efekty są tak małe, że jak na razie dają tylko górne ograniczenie na pierwotne pole magnetyczne.
 
Po rekombinacji ok. 1 milionowa materii została wciąż zjonizowana i ona przeniosła informację o pierwotnym, wielkoskalowym polu magnetycznym, które obserwujemy w CMB
 
2. Generacja PMF :
Generowanie pola magnetycznego opisuje się tradycyjnie mechanizmem baterii Biermanna (Biermann battery). Efekt ten pozwala wytworzyć pole magnetyczne rzędu 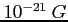$10^{-21}~G$ w rejonach, które później zapadły się w galaktyki. Polega on na wytworzeniu pola z pierwotnych wirowości, które powstały gdy niejednorości gęstości wzrosły do ok. 0.1, przez to wygenerowały szok, który kolejno ogrzewał materie i ``popychał`` ją z różnych pierwotnych źródeł szoku tworząc wiry.
 
Przy braku dyspersji (co jest charakterystyczne dla małych pól) oraz bez założeń idealnej magnetohydrodynamiki (np. separacja ładunków) równanie indukcji można zapisać jako:

$$\frac{\delta \vec{B}}{\delta t} = \vec{\bigtriangledown} \times (... ...ngledown p \times \bigtriangledown \rho}{\rho^2}\frac{c m_h}{e}\frac{1}{1+\chi}$$

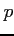$p$ - ciśnienie
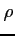$\rho$ - gęstość
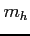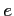$m_h$, $e$ - masa i ładunek elektronu
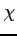$\chi$ - stopień jonizacji
 
Zazwyczaj 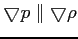$\bigtriangledown p \parallel \bigtriangledown \rho$, ale w ogólnym przypadku tak nie jest np. przy występowaniu wirowości ( 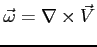$\vec{\omega}=\nabla \times \vec{V}$). Ogólne równanie wirowości można zapisać wzorem:

$$\frac{\delta \vec{\omega}}{\delta t} = \vec{\bigtriangledown} \ti... ...n p \times \bigtriangledown \rho}{\rho^2} + \nu \bigtriangledown^2 \vec{\omega}$$

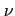$\nu$ - dyfuzyjność
 
Ponieważ od czasu powstania 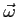$\vec{\omega}$ jest mniej więcej stała w czasie, a dyfuzyjność początkowo jest zaniedbywalna to istotny zostają tylko pierwszy i drugi wyraz po prawej stronie. A zatem następuje generacja pola aż do saturacji tego efektu.
 
Wygenerowane przez wirowość pole jest szacowane na:

$$\vec{B} = 10^{-4} \vec{\omega}$$

Pole magnetyczne wyraża się w Gaussach, a 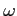$\omega$ w Hertzach. Równanie jest prawdziwe dopóki efekty przewodzenia i dyfuzji nie staną się istotne.
 
Tak wytworzone pole uległo potem uporządkowaniu. Jak B rośnie to pole w małych wirach opiera się wzmocnieniu i całkowite pole magnetyczne wzmacnia się proporcjonalnie do małych hydrodynamicznych wirów. Jednak dalej ze wzrostem pola małe wiry zostają przyciszone z powodu odprowadzania energii do pola magnetycznego. W końcu pole zostaje rozciągnięte na duże skale i tylko największe wiry przetrwają.
 
Inne konkurencyjne teorie:
- pole powstaje najpierw w gwiazdach i w czasie wybuchów supernowych jest dodawane do ISM, a następnie w wyniku mechanizmu dynama, się porządkuje
- pola najpierw pojawiają się w bardzo poczerwienionych AGN, gdzie skala czasowa wzmocnień jest o wiele krótsza. Następnie jety wyrzucają pole na zewnątrz
- wytworzenie pola w erze inflacji w czasie takiego egzotycznego zjawiska jak stworzenie pola kwantowego, przejścia fazowego przy złamaniu symetrii i rozdzieleniu sił elektrosłabych czy przez defekty topologiczne