Mierzony parametr to residuum tj. różnica między czasem przyjścia pulsu z teorii, a obserwacji. Czas z teorii musi zawierać ruch Ziemi wokół Słońca, ruch własny, może się okazać, że układ podwójny keplerowski i wtedy jego wpływ czy efekty relatywistyczne (np. tzw. opóźnienie Shapiro związane z zakrzywianiem promieniowania przez drugie ciało). Podstawowym zaś parametrem jest okres pulsacji pulsara.
1. Podstawowe parametry
Pole magnetyczne:
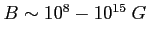
Okresy:
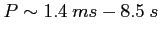
Zmiana okresu:
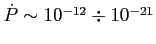
Masa:
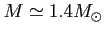
Promień:
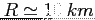
Gęstość:
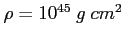
Jeśli wiek charakterystyczny
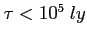 to pulsar często znajdowany razem z SNR.
to pulsar często znajdowany razem z SNR.
Emisja spójna (coherent) , co wyjaśnia ogromną jasność pulsarów tj. elektrony nie emitują niezależnie, ale w fazie. Obszary spójności maleją na wyższych częstotliwościach stąd bardzo strome widmo (generalnie
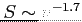 ).
).
Pulsary milisekundowe to pulsary mające towarzysza (zazwyczaj biały karzeł), który ponownie rozpędza pulsar przez co pomimo niskiego pola magnetycznego ma on bardzo krótki okres dla pulsów.
Czułość radiometru dla obserwacji pulsarów:
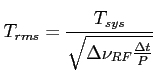
Przykładowe parametry do wyznaczenia:
a) minimalna gęstość:
Z równania, gdzie siła dośrodkowa przeważa lub równa się sile grawitacji.
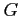 - stała grawitacji
- stała grawitacji
 - okres
- okres
np. dla mgławicy Karb
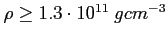 .
.
b) Zmiana prędkości kątowej:
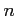 - parametr hamowania zależny od modelu
- parametr hamowania zależny od modelu 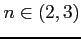
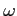 - prędkość kątowa
- prędkość kątowa
Parametr hamowania można wyznaczyć że wzoru:
Zakładamy dipolowe pole magnetyczne tj. n=3
c) Zmiana energii rotacji:
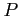 - okres pulsów,
- okres pulsów, ![$ [s]$](img512.png)
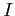 - moment bezwładności (dla kuli
- moment bezwładności (dla kuli 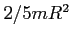 )
)
d) Minimalne pole magnetyczne:
Malenie prędkości rotacji oznacza spadek energii rotacji, która musi się odbywać w jakiś sposób. Jako, że wiadomo, że gwiazda kolapsując zatrzymała swoje pole magnetyczne, to jest ono głównym kandydatem. Zatem zakłada się, że energia zostaje wypromieniowana przez magnetyczny dipol. Daje to minimalne pole:
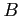 - indukcja magnetyczna na powierzchni gwiazdy,
- indukcja magnetyczna na powierzchni gwiazdy, ![$ [G]$](img116.png)
e) Wiek charaktyerystyczny (gdy
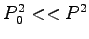 ):
):
Ośrodek międzygwiazdowy (ISM).
Im niższa częstotliwość tym większe opóźnienie z przyjściem sygnału. Jest to ściśle związane z dyspersją ośrodka międzygwiazdowego (plazma o niskiej gęstości, w której pole elektryczne przyśpiesza wolne elektrony, oscyluje z częstotliwością plazmy)
Można wyznaczyć tę częstotliwość (dla 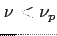 fala nie może przejść przez ośrodek):
fala nie może przejść przez ośrodek):
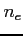 - gęstość elektronowa, typowa dla ISM to
- gęstość elektronowa, typowa dla ISM to
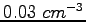
Druga zaś wielkością opisującą ISM jaka w prosty sposób można wyznaczyć to składowa radialna pola magnetycznego. Jeśli z obserwacji wyznaczymy jednocześnie miarę rotacji i dyspersji tj. RM i DM to można ta wielkość wyznaczyć bez robienia dodatkowych założeń (np. dotyczących gęstości elektronowej) W Gaussach wynosi ona:
2. Układy podwójne:
W przypadku pulsarów znajomość mas obu składników pozwala wyznaczyć 5 standardowych parametrów orbity (zrzutowana półoś wielka
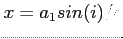 , długość perycentrum
, długość perycentrum 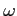 , moment przejścia przez perycentrum
, moment przejścia przez perycentrum 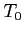 , okres orbitalny
, okres orbitalny 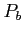 i ekscentryczność
i ekscentryczność 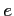 ) jak i 5 parametrów określających zmianę tej orbity związaną z efektami grawitacyjnymi (zawężanie orbity). W praktyce oznacza to, że układy podwójne pozwalają z ogromną dokładnością ocenić masy gwiazd neutronowych oraz testować ogólną teorię względności.
) jak i 5 parametrów określających zmianę tej orbity związaną z efektami grawitacyjnymi (zawężanie orbity). W praktyce oznacza to, że układy podwójne pozwalają z ogromną dokładnością ocenić masy gwiazd neutronowych oraz testować ogólną teorię względności.
3. Diagram 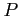 -
-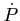 dla pulsarów:
dla pulsarów:
4. Pierwszy pozasłoneczny układ planetarny
Pierwszy pozasłoneczny układ planetarny został odkryty w 1994 roku przez Aleksandra Wolszczana. Układ ten tworzył pulsar PSR 1257+12 i został on odkryty właśnie przez pomiary opóźnień sygnału radiowego.
Obecnie sądzi się, że w układzie znajdują się trzy planety:
- półoś wielka 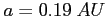 , masa , masa
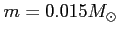 , ,
- 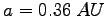 . i . i
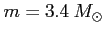 , ,
- 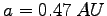 i i
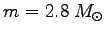 . .
![\includegraphics[width=6cm]{Newpicture/Wolszczan2.eps}](img995.png)
|
|
![\includegraphics[width=6cm]{Newpicture/Wolszczan.eps}](img996.png) |
Bogna Pazderska
2009-01-20
![]()
![]()
![]()
![]()
![]()
![]()
![]() to pulsar często znajdowany razem z SNR.
to pulsar często znajdowany razem z SNR.
![]() ).
).
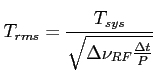
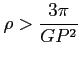
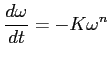
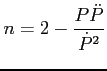
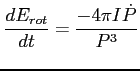
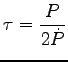
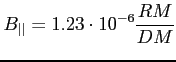
![\includegraphics[width=12cm]{Newpicture/P_dotP_pulsarDiagPL.eps}](img988.png)
![\includegraphics[width=6cm]{Newpicture/Wolszczan.eps}](img996.png)