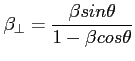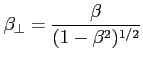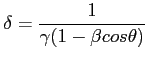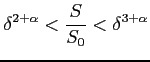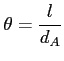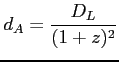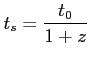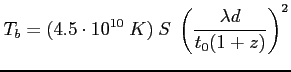a) Dla źródeł pozagalaktycznych należy wziąć poprawkę na to, że źródło porusza się z relatywistyczną prędkością względem obserwatora i obserwowana prędkość może być nawet kilkakrotnie większa niż prędkość światła (superluminal velocities). Do tego dla źródeł rozciągłych np. 2 jetów każdy z jetów ma do pokonania inną drogę do obserwatora i może mieć różne prędkości.
Obserwowana prędkość np. jetów (dokładnie V/c) wynosi:
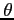 - kąt między prostą obserwator - źródło, a kierunkiem prędkości np. jetów
- kąt między prostą obserwator - źródło, a kierunkiem prędkości np. jetów
Dla określonego 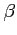 kąt przy którym obserwuje się maksymalną wartość obserwowanego
kąt przy którym obserwuje się maksymalną wartość obserwowanego
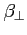 :
:
Zjawisko widziane na obserwowanej częstotliwości:
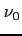 - wyemitowana częstotliwość
- wyemitowana częstotliwość
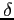 - czynnik Dopplera
- czynnik Dopplera
Gdzie czynnik Dopplera wynosi:
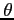 - kąt między prostą obserwator - źródło, a kierunkiem prędkości
Przykłady:
- kąt między prostą obserwator - źródło, a kierunkiem prędkości
Przykłady:
Największy czynnik Dopplera ( czyli ruch na obserwatora):
czyli ruch na obserwatora):
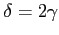
Najmniejszy czynnik Dopplera (
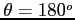 ):
):
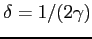
b) Obserwowany strumień:
Wpływ na strumień przy izotropowej emisji zależy od modelu, ale wiadomo, że leży w zakresie:
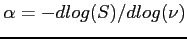 - (negatywny) indeks spektralny
- (negatywny) indeks spektralny
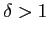 - wzmocnienie
- wzmocnienie
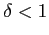 - osłabienie
- osłabienie
Zazwyczaj wystarczy przybliżenie:
c) Obserwowany rozmiar kątowy:
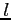 - liniowa średnica źródła
- liniowa średnica źródła
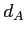 - kątowa średnica-odległość (angular diameter distance)
- kątowa średnica-odległość (angular diameter distance)
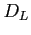 - odległość jasnościowa (
- odległość jasnościowa (
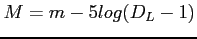 )
)
d) Dla źródeł pozagalaktycznych relatywistyczna transformacja czasu:
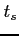 - czas związany z układem źródła
- czas związany z układem źródła
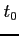 - czas obserwowany
- czas obserwowany
e) Oszacowanie min. temperatury jasnościowej (zał. zaniedbanie ruchów własnych i związany z nim efekt Dopplera) - podstawienie do wzoru na 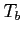 przy danym rozmiarze źródła:
przy danym rozmiarze źródła:
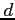 - odległość do obiektu,
- odległość do obiektu, ![$ [Mpc]$](img672.png)
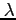 - długość fali,
- długość fali, ![$ [cm]$](img117.png)
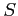 - gęstość strumienia,
- gęstość strumienia, ![$ [Jy]$](img674.png)
f) Inne relatywistyczne poprawki:
Wielkości obserwowane (z apostrofem wielkości w układzie źródła):
- kąt sferyczny:
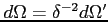
- odcinek czasu:
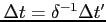
- częstotliwość:
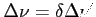
- gęstość strumienia:
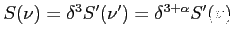
- moc: 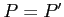
- składowa || przyśpieszenia:
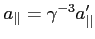
- składowa 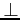 przyspieszenia:
przyspieszenia:
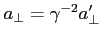
Bogna Pazderska
2009-01-20