Równanie fali poprzecznej rozchodzącej się wzdłuż osi z:
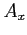 ,
, 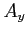 - amplitudy drgań w wyznaczonych kierunkach
- amplitudy drgań w wyznaczonych kierunkach
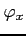 ,
, 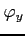 - przesunięcia fazowe drgań
- przesunięcia fazowe drgań
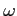 - częstość kołowa
- częstość kołowa
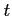 - czas
- czas
Każdą taką falę można zapisać jako sumę dwóch polaryzacji liniowych lub kołowych:
| Polaryzacja liniowa |
Polaryzacja kołowa |
|---|
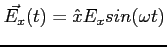 |
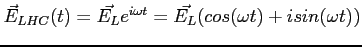 |
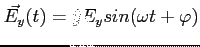 |
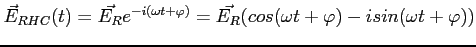 |
![\includegraphics[width=2cm]{Rysunki/Polaryzacja_liniowa_schemat.eps}](img34.png) |
![\includegraphics[width=2cm]{Rysunki/Polaryzacja_kolowa_schemat.eps}](img35.png) |
Bogna Pazderska
2009-01-20
![\includegraphics[width=2cm]{Rysunki/Polaryzacja_liniowa_schemat.eps}](img34.png)
![\includegraphics[width=2cm]{Rysunki/Polaryzacja_kolowa_schemat.eps}](img35.png)