Next: Czułość anteny (antenna sensibility) Up: Antena Previous: Rozdzielczość czasowa (Nyquist limit) Spis rzeczy
Jest to temperatura jaką miałby opornik generujący taką samą moc spektralną co nadająca antena (prawie wszystkie własności anteny nadawczej i odbiorczej są takie same). Zatem dla urządzeń jest to jednocześnie temperatura równoważna. Nie jest to zatem żadna fizyczna temperatura anteny. Używa się tej wielkości, gdyż pozwala na łatwe porównania z urządzeniami systemowymi jak i z rezystorami, które używa się do kalibracji sygnału. Zawsze liczy się dla pojedynczej polaryzacji (generalnie kołowej).
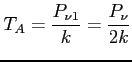
Dla źródła dyskretnego, niespolaryzowanego: związek z temperaturą jasnościową i rozmiarami źródła:
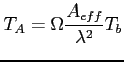
Dla źródła rozciągłego, niespolaryzowanego (rozmiary wiązki porównywalne z rozmiarami źródła):
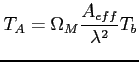
Ogólny związek z temperaturą jasnościową (źródło niespolaryzowane):
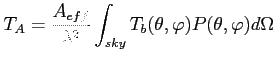
Przybliżenie dla źródła dyskretnego:
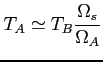
Przybliżenie dla źródła rozciągłego:
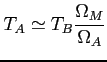
Bogna Pazderska 2009-01-20