Na antenie powstaje fala stojąca w wyniku której wewnątrz niej indukuje się prąd elektryczny. Opis własności anteny może być dokonany przez funkcję natężenia (I), rozkład wartości wektora natężenia pola elektrycznego (E) czy rozkład wyemitowanej mocy (P), wszystko dla określonej częstotliwości.
Współrzędne:
Zatem dla dowolnej anteny:
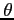 - kąt między danym kierunkiem, a osią symetrii
- kąt między danym kierunkiem, a osią symetrii
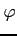 - kąt mierzony od osi x
- kąt mierzony od osi x
1. Antena dipolowa o długości l:
Indukuje się prąd:
Z formuły Larmor'a wiemy, że dla ładunku w antenie:
W antenie:
Tak można otrzymać rozkład pola elektrycznego na antenie.
Aby uzyskać moc w zależności od kąta (charakterystyka mocy) wystarczy wyliczyć wartość wektora Poyntinga uśrednioną w czasie (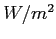 - strumień)
- strumień)
a otrzyma się zależność od kąta
Charakterystyka mocy dla anteny dipolowej:
2. Antena paraboliczna
Podobnie można wyliczyć charakterystykę mocy dla anteny parabolicznej, ale praktyce stosuje się transformatę Fouriera z dystrybucji pola elektrycznego na czaszy. Obliczona charakterystyka mocy dla kołowej powierzchni o średnicy D stanowi dobre przybliżenie.
Wielkości:
- $&bull#bullet;$
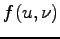 - dystrybucja napięcia na czaszy teleskopy (aperture voltage distribution), związana z patrzeniem na konkretnym kierunku
- dystrybucja napięcia na czaszy teleskopy (aperture voltage distribution), związana z patrzeniem na konkretnym kierunku
-
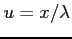 ,
,
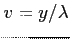 - współrzędne aperturowe (położenia ekstremów są funkcją u i v np. 1 minimum charakterystyki mocy
- współrzędne aperturowe (położenia ekstremów są funkcją u i v np. 1 minimum charakterystyki mocy
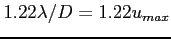 )
)
- x,y - odległości na czaszy teleskopu w obu współrzędnych (dla RT4 0-16 m )
- $&bull#bullet;$
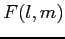 - dystrybucja rozkładu napięcia (gdyby antena nadawała to rozkład pierwiastka kwadratowego w wypromieniowanej mocy) w funkcji odległości kątowych na niebie (far-field voltage radiation pattern)
- dystrybucja rozkładu napięcia (gdyby antena nadawała to rozkład pierwiastka kwadratowego w wypromieniowanej mocy) w funkcji odległości kątowych na niebie (far-field voltage radiation pattern)
-
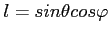 ,
,
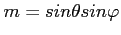 - kątowe odległości na niebie
- kątowe odległości na niebie
Przejście między oboma rozkładami dokonuje się przy użyciu transformaty Fouriera:
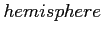 - składowa prostopadła sfery niebieskiej
- składowa prostopadła sfery niebieskiej
Natomiast by otrzymać charakterystykę mocy wyraża się wzorem:
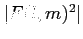 . Przy symetrii rotacyjnej (jak w antenie parabolicznej) wystarczą współrzędne: l i u. Wtedy charaterystyka mocy wynosi:
. Przy symetrii rotacyjnej (jak w antenie parabolicznej) wystarczą współrzędne: l i u. Wtedy charaterystyka mocy wynosi: 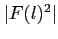 .
.
Najprostszy przypadek, przy równomiernym oświetleniu całej apertury jest pokazany na rysunku (apertura i jej obraz wraz z przekrojem poprzecznym oświetlenia i jego obraz, który też stanowi odpowiedz anteny na pojedyńczy punkt):
Bardziej rzeczywisty rozkład napięcia na czaszy i charakterystykę mocy prezentuje rysunek:
Rozkład kątowy przy patrzeniu na źródło o jasności
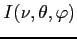 pokazuje rysunek (dla źródła dyskretnego, moc pochodząca że źródła zmienia tylko amplitudę rozkładu pola elektrycznego na antenie, nie zmienia zaś jej kształtu):
pokazuje rysunek (dla źródła dyskretnego, moc pochodząca że źródła zmienia tylko amplitudę rozkładu pola elektrycznego na antenie, nie zmienia zaś jej kształtu):
Najczęściej korzysta się że znormalizowanej charakterystyki mocy, którą w funkcji kątów można zapisać:
Dla RT4 można dla głównej wiązki przybliżyć ją wzorem:
Zazwyczaj wystarczy jednak przybliżenie:
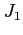 - funkcje Bessela pierwszego rodzaju (dla rozkładu pola równomiernego)
- funkcje Bessela pierwszego rodzaju (dla rozkładu pola równomiernego)
![\includegraphics[width=3cm]{Rysunki/BesselJ.eps}](img357.png)
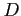 - średnica reflektora głównego
- średnica reflektora głównego
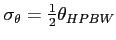 - szerokość połówkowa wiązki anteny na danej częstotliwości
- szerokość połówkowa wiązki anteny na danej częstotliwości
(np. dla fali 5 cm
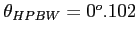 stąd
stąd
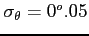 )
)
Zaś rozkład mocy na powierzchni czaszy (związanej z patrzeniem w danym kierunku):
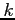 - współczynnik, dla RT4 około
- współczynnik, dla RT4 około
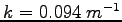
(wyliczone z tego, że na brzegu czaszy tłumienie 12 dB)
x - odległość od osi ![$ [m]$](img110.png) , dla RT4
, dla RT4
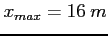
Dla RT4 na 1660 MHz, charakterystyka napięcia i mocy:
Charakterystyka mocy determinuje wielkości opisujące antenę jak: rozdzielczość kątowa, pełną szerokość wiązki, wzmocnienie anteny (kierunkowość), która wpływa na aperturę efektywną.
Bogna Pazderska
2009-01-20
![\includegraphics[width=5cm]{Rysunki/Spherical-coordinates.eps}](img316.png)
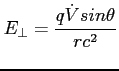
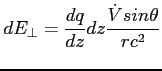
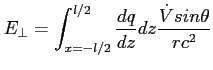
![]() - strumień)
- strumień)
![\includegraphics[width=4cm]{Rysunki/ant_hwave.eps}](img326.png)
![\includegraphics[width=4cm]{Rysunki/ant_hwave_azimuth.eps}](img327.png)
![\includegraphics[width=4cm]{Rysunki/ant_hwave_elevation.eps}](img328.png)
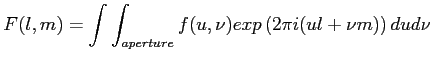
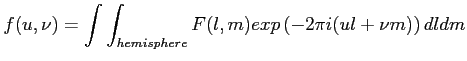
![\includegraphics[width=7cm]{Interferometr/uvw.eps}](img339.png)
![\includegraphics[width=8cm]{Interferometr/aper_beam.eps}](img342.png)
![\includegraphics[width=8cm]{Interferometr/pattern.eps}](img343.png)
![\includegraphics[width=9cm]{Interferometr/AntenaPT.eps}](img345.png)
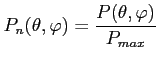
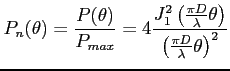
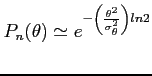
![]() - funkcje Bessela pierwszego rodzaju (dla rozkładu pola równomiernego)
- funkcje Bessela pierwszego rodzaju (dla rozkładu pola równomiernego)
![\includegraphics[width=3cm]{Rysunki/BesselJ.eps}](img357.png)
![]() - średnica reflektora głównego
- średnica reflektora głównego
![]() - szerokość połówkowa wiązki anteny na danej częstotliwości
- szerokość połówkowa wiązki anteny na danej częstotliwości
![]() stąd
stąd
![]() )
)
![]() - współczynnik, dla RT4 około
- współczynnik, dla RT4 około
![]()
![]() , dla RT4
, dla RT4
![]()
![\includegraphics[width=8cm]{Rysunki/CharMocyRT4.eps}](img356.png)