Wewnętrzna emisja i absorpcja

Równanie przepływu:
Najogólniejsza postać:

$$\frac{dI_\nu}{ds} = -\alpha_\nu I_\nu + j_\nu$$

W innej postaci:

$$\frac{dI_\nu}{d\tau_\nu} = - I_\nu + S_\nu$$

Gdzie $S_\nu$ - funkcja źródła, zdefiniowana jako:

$$S_\nu = \frac{j_\nu(T)}{\alpha_\nu(T)}$$

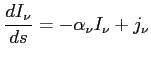
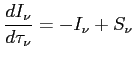
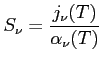
W przypadku lokalnej równowadze termodynamicznej (LTE) z prawa Kirchhoffa:

$$S_\nu = B_\nu (T) = \frac{j_\nu(T)}{\alpha_\nu(T)} = B_i$$

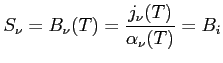
Połączenie emisji i absorpcji dla samej chmury daje jasność (obserwowaną) - rozwiązanie równania przepływu dla emisji termicznej (LTE):

$$B_o = B_i \left( {1-e^{-\tau_c}}\right)$$

$B_i$ - jasność chmury z prawa Kirchhoffa

Po przypisaniu temperatury z przybliżenia R-J:

$$T_b = T_c \left( {1-e^{-\tau_c}}\right)$$

$T_b$ - temperatura jasnościowa, obserwowana
$T_c$ - temperatura obłoku (elektronowa,..) (np. PN, SNR czy obłoki molekularne)

Podział ośrodków że względu na głębokość optyczną:

(1)  $\tau_c \ll 1$ - chmura przezroczysta (transparent), optycznie cienka (opticaly thin)
(2)  $\tau_c \simeq 1$ - pośrednia sytuacja
(3)  $\tau_c \gg 1$ - chmura nieprzezroczysta (opaque), optycznie gruba (opticaly thick)
 
Stąd przybliżone wartości obserwowanych jasności:

- optycznie cienki: $B_o \simeq B_i \tau_c = \frac{j_\nu(T)}{\alpha_\nu(T)} \alpha (T) x_k = j_\nu(T) x_k$
- optycznie gruby: $B_o \simeq B_i= \frac{j_\nu(T)}{\alpha_\nu(T)}$