Next: Emisja Up: Absorpcja i emisja energii Previous: Absorpcja i emisja energii Spis rzeczy
Zachodzi, gdy fala przechodzi przez ośrodek, który ją absorbuje (co jest związane z tłumieniem (attenuation) np. chmury czy atmosfery). Opisuje się to przez grubość optyczną, inaczej nieprzezroczystość (optical depth, opacity):
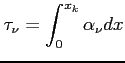
Ogólnie
![]() , gdzie
, gdzie ![]() współczynnik transmisji (transmission coefficient) i
współczynnik transmisji (transmission coefficient) i
Wtedy gęstość strumienia i jasność po przejściu przez chmurę ma wartość:
np. ![]() oznacza, że gęstość strumienia została zredukowana do 1/e pierwotnej wartości
oznacza, że gęstość strumienia została zredukowana do 1/e pierwotnej wartości
Często stosuje się skale decybelową:
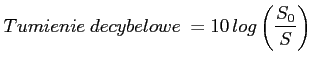
Rysunek przedstawia temperaturę systemową w funkcji elewacji (wysokości) i częstotliwości, gdzie widać wkład od atmosfery:
![\includegraphics[width=6cm]{Rysunki/TempSzumowa.eps}](img258.png)
Stosujemy płaski model atmosfery, zatem droga przez jaką będzie przechodzić fala zależy od odległości zenitalnej (z):
Ponieważ dla
![]() poza linią wody na 22 GHz (gdzie
poza linią wody na 22 GHz (gdzie ![]() od 0.1 do 0.2 w zależności od wilgotności powietrza)
od 0.1 do 0.2 w zależności od wilgotności powietrza)
![]() to można zastosować przybliżenie:
to można zastosować przybliżenie:
Zatem atmosfera pochłania
![]() - czyli wielkość proporcjonalną do temperatury jasnościowej atmosfery. Stąd
- czyli wielkość proporcjonalną do temperatury jasnościowej atmosfery. Stąd
![]() .
.
Wystarczy pomierzyć temp. systemowe na 2 różnych odległościach zenitalnych (temperatura atmosfery na danej odległości zenitalnej + stała temperatura całej reszty) by móc wyliczyć głębokość optyczną.
Otrzymanie ![]() z pomiarów czynionych przez radioteleskop:
z pomiarów czynionych przez radioteleskop:
Bogna Pazderska 2009-01-20