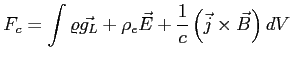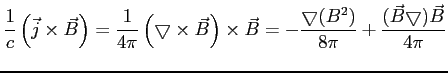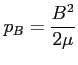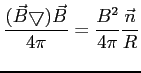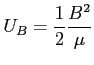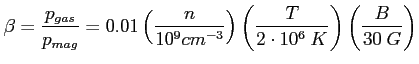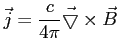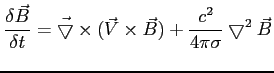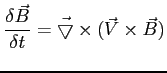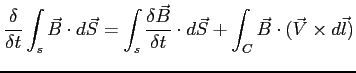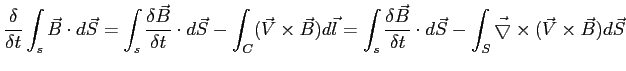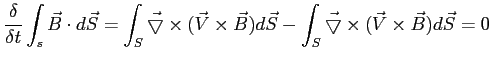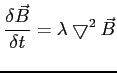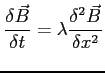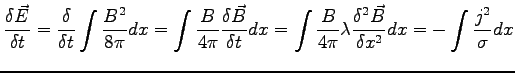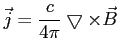Właściwości

Podstawowe wielkości i związek między nimi:

$$\vec{B}=\mu \vec{H}$$

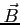$\vec{B}$ - wektor indukcji (gęstość strumienia magnetycznego lub pole magnetyczne), $[T]$ lub 
     cgs: gauss $[G]$
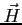$\vec{H}$ - natężenie pola magnetycznego, $[A/m]$ lub cgs: oersted $[Oe]$
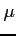$\mu$ - przenikalność magnetyczna ośrodka
 
1. Siła działająca na naładowaną cząstkę (SI):

$$\vec{F_L}=q(\vec{V} \times \vec{B})$$

Całkowita siła działająca na ciało:

$$F_c= \int \varrho \vec{g_L}+\rho_e\vec{E} +\frac{1}{c} \left( {\vec{j}\times \vec{B}}\right) dV$$

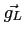$\vec{g_L}$ - lokalne przyśpieszenie grawitacyjne
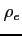$\rho_e$ - wypadkowa gęstość ładunków elektrycznych (w plaźmie $\rho_e=0$)
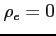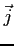$\vec{j}$ - gęstość prądu elektrycznego
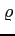$\varrho$- gęstość elementu
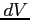$dV$ - element objętości
 
Składową siły związaną z polem magnetycznym tj. siłę Lorentza można zapisać w przypadku nierelatywistycznym (wtedy z prawa Ampere'a 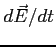$d\vec{E}/dt$ - zaniedbywalne i 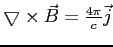$\bigtriangledown \times \vec{B} =\frac{4\pi}{c}\vec{j}$) jako:

$$\frac{1}{c} \left( {\vec{j}\times \vec{B}}\right) = \frac{1}{4\pi... ...\bigtriangledown (B^2)}{8\pi} + \frac{(\vec{B}\bigtriangledown) \vec{B}}{4 \pi}$$

Pierwszy składnik interpretuje się jako gradient ciśnienia magnetycznego, zaś drugi jako naprężenie pola magnetycznego.
 
a) Ciśnienie magnetyczne:

$$p_B=\frac{B^2}{2\mu}$$

Gradient ciśnienia magnetycznego ze znakiem ujemnym stanowi składnik siły Lorentza, siły skierowanej przeciwnie do wzrostu pola magnetycznego.
 
b) Naprężenie pola manetycznego:

$$\frac{(\vec{B}\bigtriangledown) \vec{B}}{4 \pi}=\frac{B^2}{4\pi}\frac{\vec{n}}{R}$$

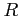$R$ - promień krzywizny linii pola
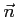$\vec{n}$ - wektor jednostkowy, prostopadły do linii, styczny do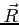 $\vec{R}$
 
Naprężenie magnetyczne prostuje linie pola i rośnie wraz ze wzrostem zakrzywienia. Generalnie obie składowe siły Lorentza są przeciwnie względem siebie skierowane.
 
2. Gestość energii pola magnetycznego:

$$U_B=\frac{1}{2}\frac{B^2}{\mu}$$

 
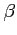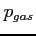3. Parametr plazmy $\beta$:

$$\beta=\frac{p_{gas}}{p_{mag}}=0.01\left( \frac{n}{10^9cm^{-3}}\right) \left( \frac{T}{2\cdot 10^6~K}\right) \left( \frac{B}{30~G}\right)$$

$p_{gas}$ - ciśnienie gazu
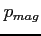$p_{mag}$ - ciśnienie pola magnetycznego
 
4. Gestość prądu indukcyjnego:

$$\vec{j}=\frac{c}{4\pi}\vec{\bigtriangledown} \times \vec{B}$$

Jest to wartość w przypadku nierelatywistycznym, gdy zmiana 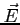$\vec{E}$ w czasie jest zaniedbywalna.
 
5. Ogólne równanie opisujace zachowanie pola magnetycznego (równanie indukcji):

$$\frac{\delta \vec{B}}{\delta t} = \vec{\bigtriangledown} \times (\vec{V} \times \vec{B}) + \frac{c^2}{4\pi \sigma}\bigtriangledown^2 \vec{B}$$

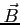$\vec{B}$ - indukcja magnetyczna
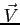$\vec{V}$ - prędkość ruchu ośrodka (pola)
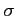$\sigma$ - współczynnik przewodnictwa
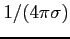$1/(4\pi \sigma)$ - dyfuzyjność magnetyczna ośrodka (proporcjonalna do oporu ośrodka)
 
Pierwszy składnik po prawej stronie opisuje zjawisko sprzężenia pola magnetycznego z ośrodkiem doskonale przewodzącym prąd (zmiany pola związane są wyłącznie z jego przenoszeniem z miejsca na miejsce). Zaś drugi składnik opisuje dyfuzje pola.
 
a) Wmrożenie pola:
W bardzo dobrze przewodzących ośrodkach:

$$\frac{\delta \vec{B}}{\delta t} = \vec{\bigtriangledown} \times (\vec{V} \times \vec{B})$$

 
Tempo zmiany strumienia magnetycznego przez powierzchnię S (o brzegu C, będącą krzywą zamkniętą) może być związane ze zmianą samego pola (pierwszy wyraz), bądź ze zmianą powierzchni (drugi wyraz):

$$\frac{\delta }{\delta t} \int_s \vec{B} \cdot d\vec{S} = \int_s \... ...B}}{\delta t} \cdot d\vec{S} + \int_C \vec{B} \cdot (\vec{V} \times d\vec{l} )$$

Korzystając z tw. Stokesa dla 2 wyrazu:

$$\frac{\delta }{\delta t} \int_s \vec{B} \cdot d\vec{S} = \int_s \... ...\vec{S} -\int_S \vec{\bigtriangledown} \times (\vec{V} \times \vec{B}) d\vec{S}$$

Korzystając z równania indukcji dla 1 wyrazu (przy obecnych założeniach):

$$\frac{\delta }{\delta t} \int_s \vec{B} \cdot d\vec{S} = \int_S \... ...S} - \int_S \vec{\bigtriangledown} \times (\vec{V} \times \vec{B}) d\vec{S} = 0$$

A zatem strumień pola magnetycznego jest wmrożony w plazmę w ośrodku doskonale przewodzącym i jeżeli plazma porusza się, to pole magnetyczne porusza się razem z plazmą.
 
W typowych warunkach ISM czas dyfuzji jest bardzo duży 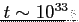$t \sim 10^{33}s$, stąd w dużych skalach pole jest doskonale wmrożone (w małych skalach nie, ze względu na duże gradienty pola magnetycznego).
 
b) Dyfuzja pola:
Jeśli w ośrodku dominuje dyfuzja to:

$$\frac{\delta \vec{B}}{\delta t} = \lambda \bigtriangledown^2 \vec{B}$$

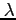$\lambda$ - współczynnik dyfuzji
 
W przypadku jednowymiarowym:

$$\frac{\delta \vec{B}}{\delta t} =\lambda \frac{\delta^2 \vec{B}}{\delta x^2}$$

Zaś zmiana energii mechaniczne w czasie jest równa:

$$\frac{\delta \vec{E}}{\delta t} = \frac{\delta }{\delta t} \int \... ...i} \lambda \frac{\delta^2 \vec{B}}{\delta x^2} dx = -\int \frac{j^2}{\sigma} dx$$

Zatem im ośrodek ma większy opór tym większa ilość energii zostaje zużyta na grzanie ośrodka (ohmic heating).
 
Okres dyfuzji ziemskiego pola magnetycznego (bez mechanizmu utrzymania pola) to 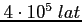$4\cdot 10^5~lat$, Słońca 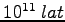$10^{11}~lat$, a Galaktyki $4\cdot 10^{23}~lat$.
 
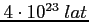6. Rekoneksja magnetyczna:
Występuje gdy plazma w obszarach o przeciwnym kierunku linii pola magnetycznego przybliża się do siebie (styczne nieciągłości) co indukuje pole elektryczne, które wywołuje prąd elektryczny:

$$\vec{j} = \frac{c}{4 \pi} \bigtriangledown \times \vec{B}$$

- w centrum znika składowa styczna pola (anihilacja pola) i energia magnetyczna ulega zmianie w ok. 50% na ciepło (prawo Ohma) i 50% na energię kinetyczną, przez co zjawisku towarzyszą silne wyrzuty materii. Widoczne jest to przede wszystkim w koronie Słonecznej.