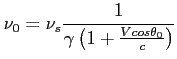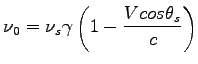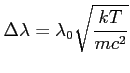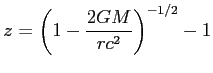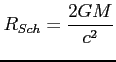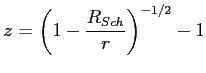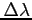 - zmiana długości fali w widmie
- zmiana długości fali w widmie
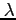 - długość laboratoryjna danego pierwiastka/molekuły
- długość laboratoryjna danego pierwiastka/molekuły
1. Związany z prędkością własną ciała (nierelatywistyczny efektu Dopplera)
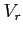 - prędkość radialna, dodatnia przy zbliżaniu
- prędkość radialna, dodatnia przy zbliżaniu
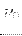 - częstotliwość obserwowana
- częstotliwość obserwowana
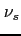 - częstotliwość wyemitowana
- częstotliwość wyemitowana
2. Rozszerzanie się Wszechświata (relatywistyczny efektu Dopplera)
a) Prędkość radialna:
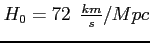
Albo:
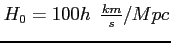 , gdzie h=0.72
, gdzie h=0.72
c) Dowolna prędkość ucieczki V (najbardziej ogólny przypadek):
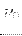 - częstotliwość obserwowana
- częstotliwość obserwowana
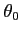 - kąt pomiędzy prędkością V, a kierunkiem obserwator - źródło w momencie wyemitowania światła przez źródło
- kąt pomiędzy prędkością V, a kierunkiem obserwator - źródło w momencie wyemitowania światła przez źródło
Lub:
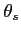 - kąt pomiędzy prędkością V, a kierunkiem obserwator - źródło w momencie odebrania światła
- kąt pomiędzy prędkością V, a kierunkiem obserwator - źródło w momencie odebrania światła
Efekt występuje również, gdy źródło nie zmienia swojej odległości od obserwatora (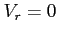 )
)
3. Poszerzenie temperaturowe linii
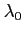 - długość centrum linii
- długość centrum linii
m - masa atomu
Oczywiście istnieje wiele czynników poszerzających linię jak np. rotacja czy silna grawitacja.
4. Zakrzywienie grawitacyjne
Obserwowana zmiana długości fali w wyniku zakrzywienia czasoprzestrzeni wokół masywnego obiektu (UKŁAD SI):
M - masa masywnego ciała
r - odległość od obiektu
Można tą wielkość zapisać przy użyciu promienia Schwarzschild'a (promień dla którego promień o danej masie jest czarną dziurą):
Wtedy:
- dla Słońca wynosi
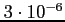
- zmierzono dla kilku białych karłów
Bogna Pazderska
2009-01-20
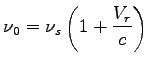
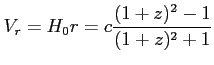
![]()
![]() , gdzie h=0.72
, gdzie h=0.72